基于粘流理论的船模阻力虚拟试验
Ship Resistance Virtual Test based on Viscous Flow Theory试验介绍
开始试验1.功能介绍
船模阻力虚拟试验是基于粘流理论进行开发的虚拟试验,试验针对三大主力船型集成了计算体网格自动生成和参数设置等专家知识库,操作简单易用,能满足船舶静水阻力的性能评估要求。
2.产品特色
1. 船模阻力系列工况的构建;
2. 集成了专家知识库,自动完成网格划分、求解器参数设定、求解计算等过程;
3. 操作简便,只需用户输入基本参数便可开始计算,减少人机交互;
4. 提供多种结果显示办法:表格、曲线、云图、报告等;
3.运行环境和效率
主流PC机上即可运行;
网页上进行任务提交,采用虚拟化技术,动态分配资源,满足计算所需。
32核并行情况,9个小时即可获得单个航速点的计算结果;
4.试验精度
船模阻力虚拟试验算法稳定可靠,计算值获得了物模试验的验证,船模阻力计算值误差在3%以内。
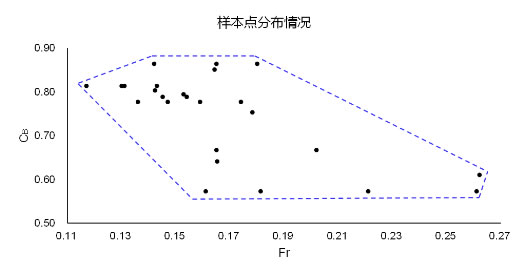
计算样本分布情况
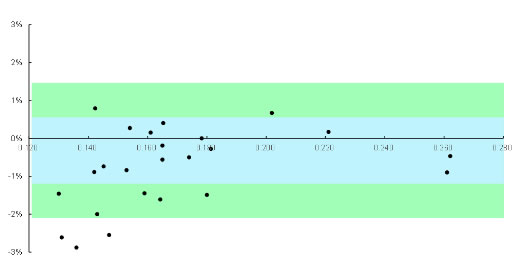
计算精度分布情况
5. 适用范围
船模阻力虚拟试验中的专家知识库是基于船模尺度下的静水阻力工况而进行开发的,针对船模静水阻力,本虚拟试验的适用范围如下:
(1) 三大主力船型;
(2) 傅汝德数范围
集装箱船的傅汝德数为0.13~0.28;
油船、散货船的傅汝德数为0.1~0.19;
(3) 方型系数范围
油船、散货船的方形系数不宜超过0.89;
集装箱船的方形系数不宜超过0.8;
(4) 甲板距离水面距离不宜超过垂线间长的3.8%;
(5) 型宽不宜超过垂线间长的18.6%;
(6) 吃水深度不宜超过垂线间长的6.25%;
(7) 艉封板到0站的距离不宜超过垂线间长的4%;
典型案例
开始试验1.典型案例一 某散货船船模阻力虚拟试验
1.1 案例名称
样例试验-某散货船船模阻力虚拟试验
1.2 案例描述
本案例以某散货船为试验对象,采用基于粘流理论的船模阻力虚拟试验进行计算,分别计算了1.09m/s(实船14kn)这个航速,同时调用了专家知识库以自动划分网格,并设置求解器相关参数。采用32个核进行计算,耗时16个小时。计算结果良好,计算精度与相应的模型试验相比,全部小于3%。操作简便,极大减少人机交互过程。
1.3 基本船型参数
| 船舶名称: | 某散货船 | 船型类型: | 散货船 |
|---|---|---|---|
| 船舶总长(m): | 335 | 船舶水线长(m): | 320 |
| 船舶垂线间长(m): | 314.6 | 桨轴距基线高(m): | 4.97 |
| 船舶型宽(m): | 52.5 | 船舶艉吃水(m): | 18.1 |
| 船舶艏吃水(m) | 18.1 | 缩尺比: | 43.636 |
| 温度(℃): | 25.7 | 测试航速(kn): | 14 |
1.4 船模几何

图2.1 船模几何
1.5 船模阻力虚拟试验
1.5.1 计算网格
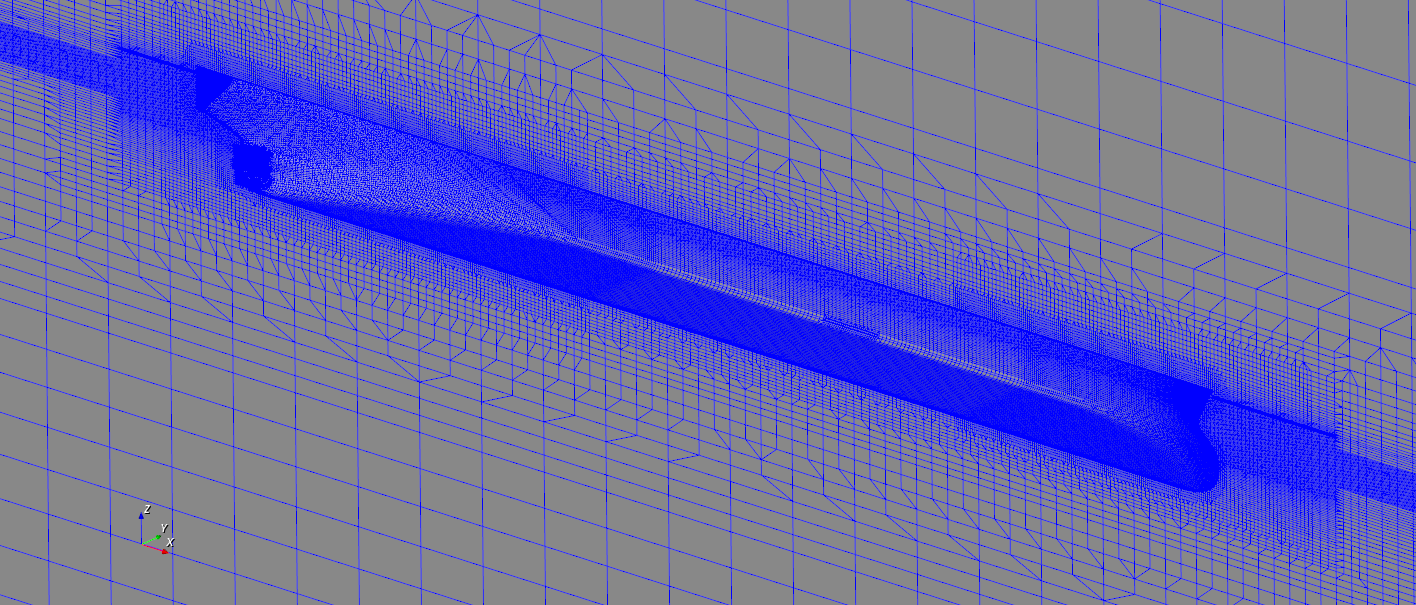
图2.2 计算网格
1.5.2 计算结果
| 速度(m/s) | 试验值(N) | 计算值(N) | 误差(%) |
|---|---|---|---|
| 1.09 | 28.882 | 29.6316 | 2.6 |
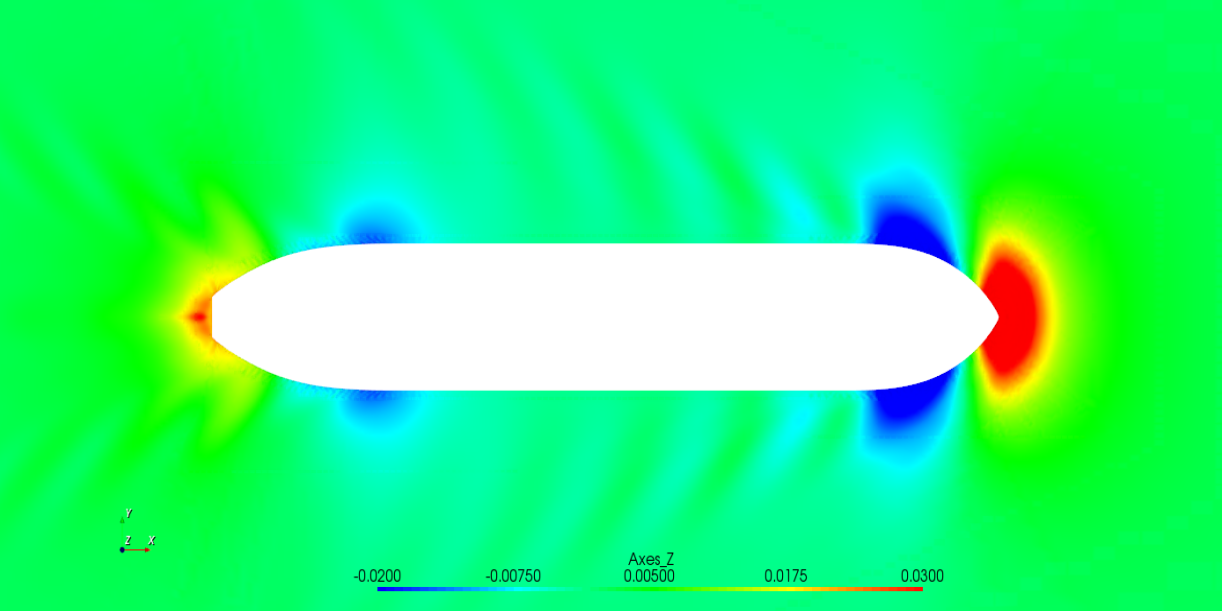
图2.3 船行波
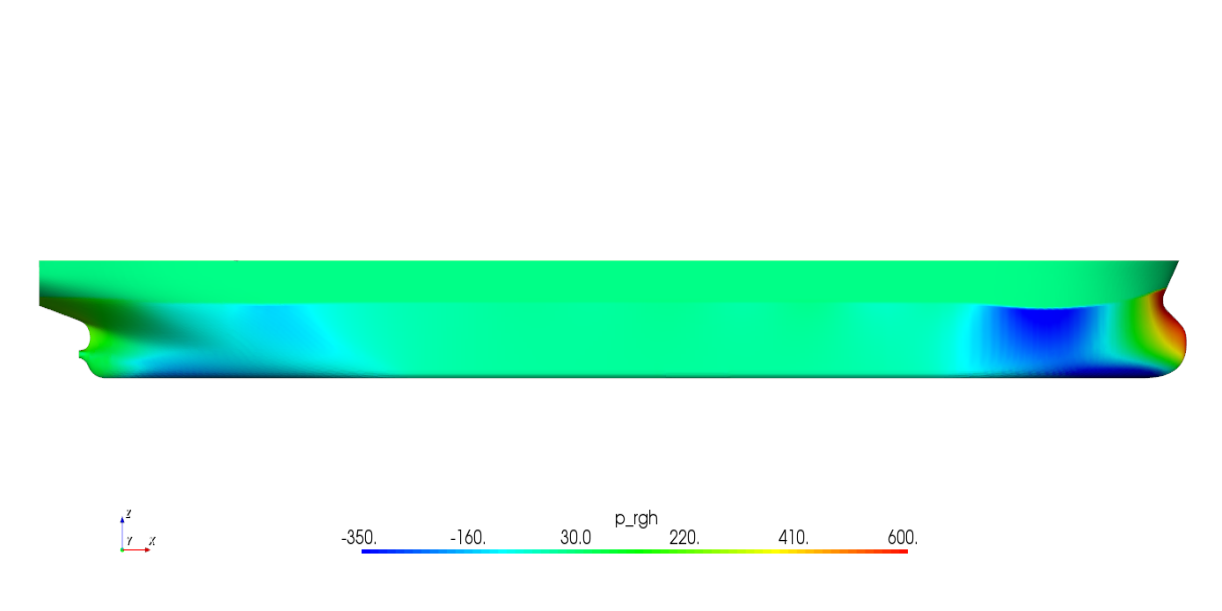
图2.4 船体表面压力分布云图
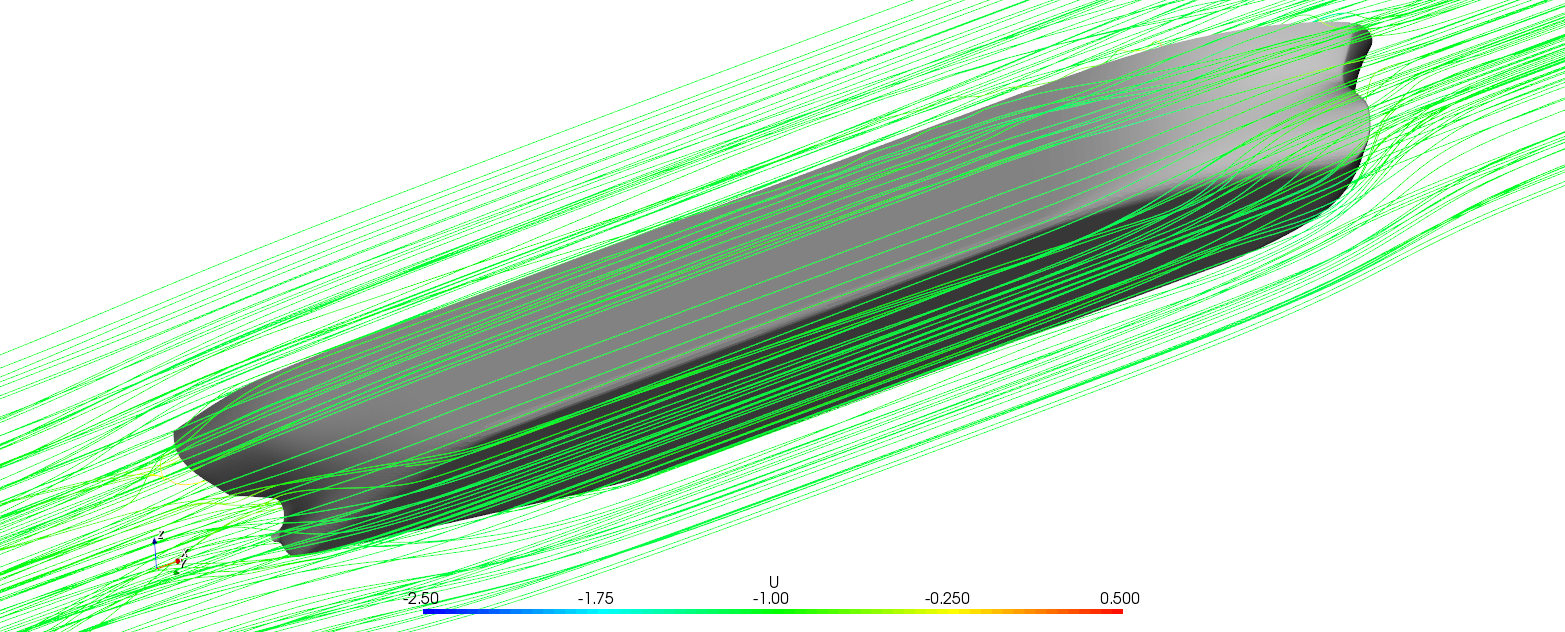
图2.5 船体周围流线
1.6 主流商业软件(starccm+)
1.6.1 计算网格

图2.6 starccm+商业软件计算网格
1.6.2 计算结果
| 速度(m/s) | 试验值(N) | 计算值(N) | 误差(%) |
|---|---|---|---|
| 1.09 | 28.882 | 28.24 | -2.3 |
图2.7 船行波
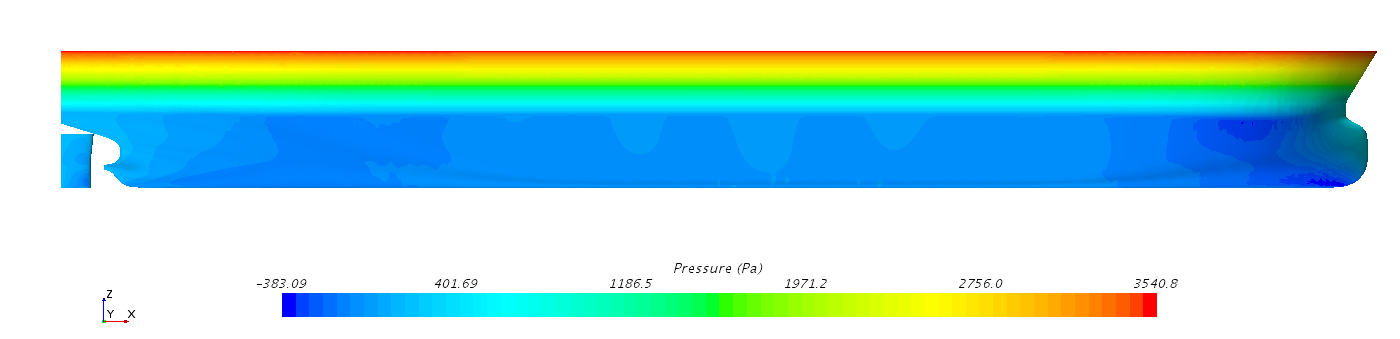
图2.8 船体表面压力分布云图
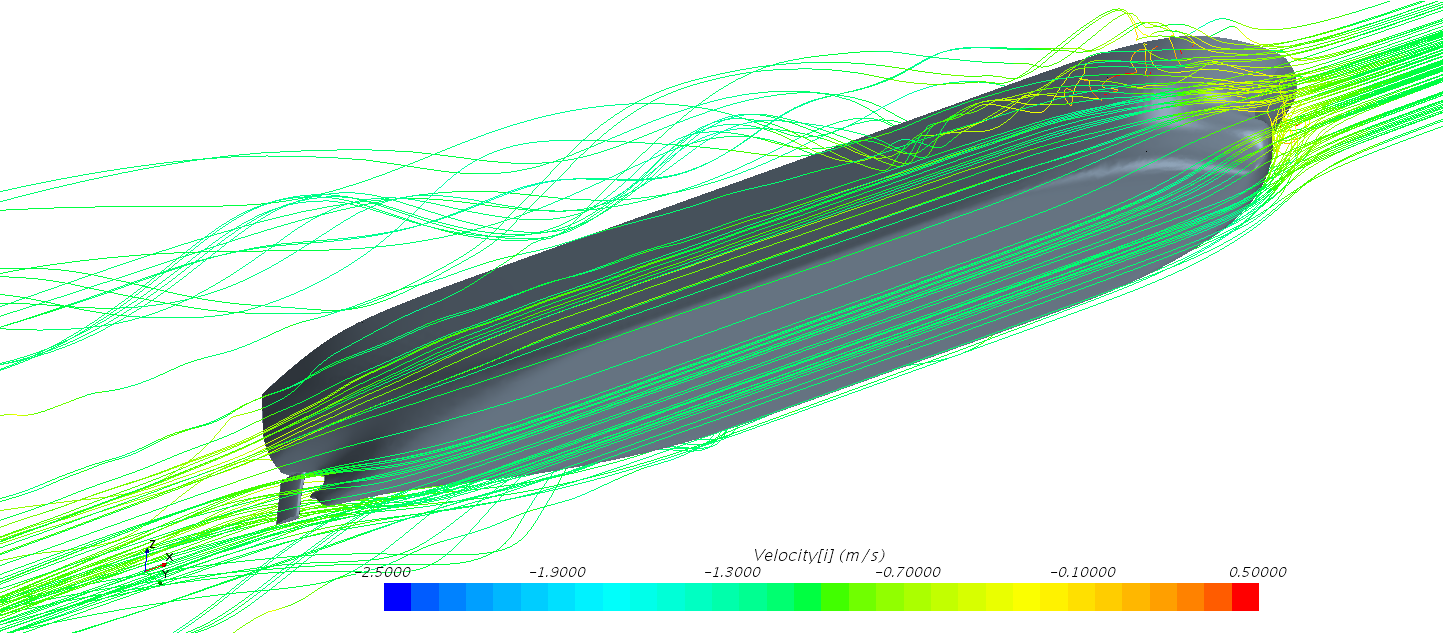
图2.9 船体周围流线
1.7 性能对比
选取某散货船作为计算对象,分别采用本虚拟试验与主流商业软件进行船模静水阻力计算,并就这两种工具进行了比对结果整理如下表:两个种方法均采用不可压缩的雷诺时均纳维—斯托克斯(Reynolds-Averaged Naiver-Stokes)方程作为控制方程,湍流模型选择为SST ;计算精度方面,两种方法的预报值与试验结果相比,计算精度相当,均在3%以内;耗时方面,本虚拟试验计算单个航速点的耗时为16个小时,商业软件Starccm+耗时较短为6.17个小时;另外,本虚拟试验中集成了专家知识库,可以一键实现网格划分及求解相关参数设置,操作简便,可以保证三大主力船型在设计航速点附近的计算精度。
| 对比项 | 虚拟试验 | Starccm+ |
|---|---|---|
| 计算方法 | RANS | RANS |
| 网格量(百万) | 2.08 | 1.58 |
| 精度(%) | 2.6 | -2.3 |
| 效率(耗时) | 16h(32核) | 6.17h(32核) |
| 专家策略 | 有 | 无 |
1.典型案例二 KCS船船模阻力虚拟试验
1.1 案例名称
样例试验-KCS船船模阻力虚拟试验
1.2 案例描述
本案例KCS船为试验对象,采用基于粘流理论的船模阻力虚拟试验进行计算,分别计算了2.196m/s(实船24kn)这个航速,同时调用了专家知识库以自动划分网格,并设置求解器相关参数。采用32个核进行计算,耗时16个小时。计算结果良好,两个工况的计算精度与相应的模型试验相比,全部小于3%。操作简便,极大减少人机交互过程。
1.3 基本船型参数
| 船舶名称: | KCS船 | 船型类型: | 集装箱船 |
|---|---|---|---|
| 船舶总长(m): | 235 | 船舶水线长(m): | 232.5 |
| 船舶垂线间长(m): | 230 | 桨轴距基线高(m): | 4.1079 |
| 船舶型宽(m): | 52.5 | 船舶艉吃水(m): | 18.1 |
| 船舶艏吃水(m) | 10.8 | 缩尺比: | 31.5995 |
| 温度(℃): | 11 | 测试航速(kn): | 24 |
1.4 船模几何

图2.10 船模几何
1.5 船模阻力虚拟试验
1.5.1 计算网格

图2.11 计算网格
1.5.2 计算结果
| 速度(m/s) | 试验值(N) | 计算值(N) | 误差(%) |
|---|---|---|---|
| 2.196 | 85.48 | 83.7486 | -2.1 |
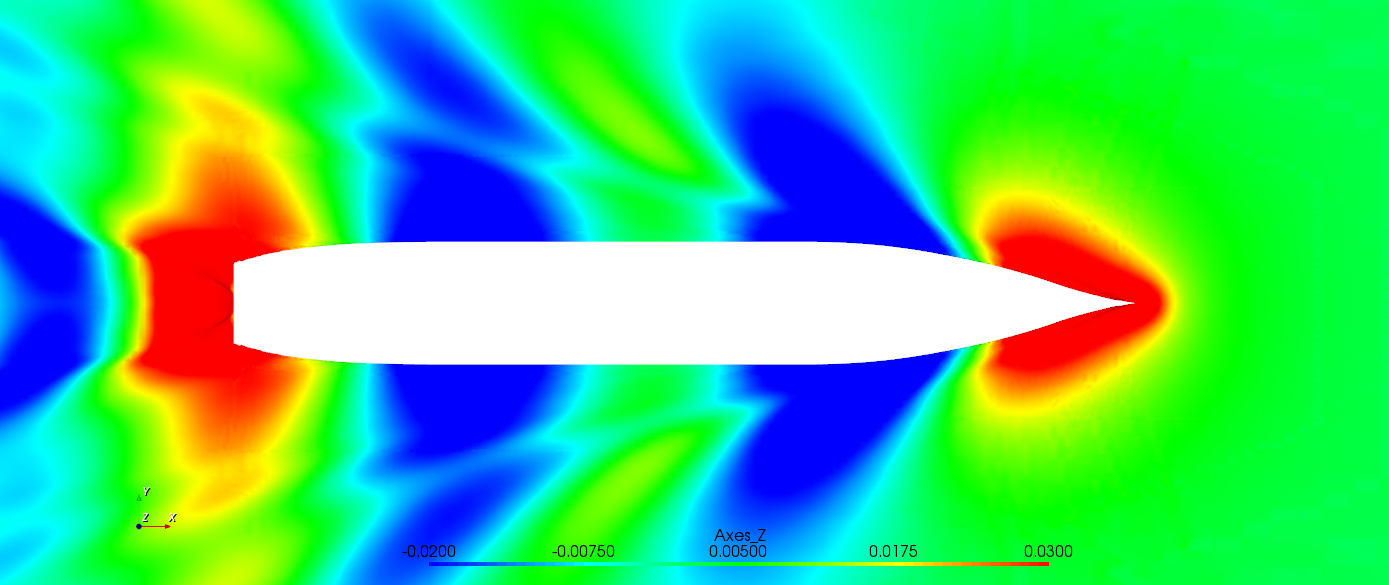
图2.12 船行波
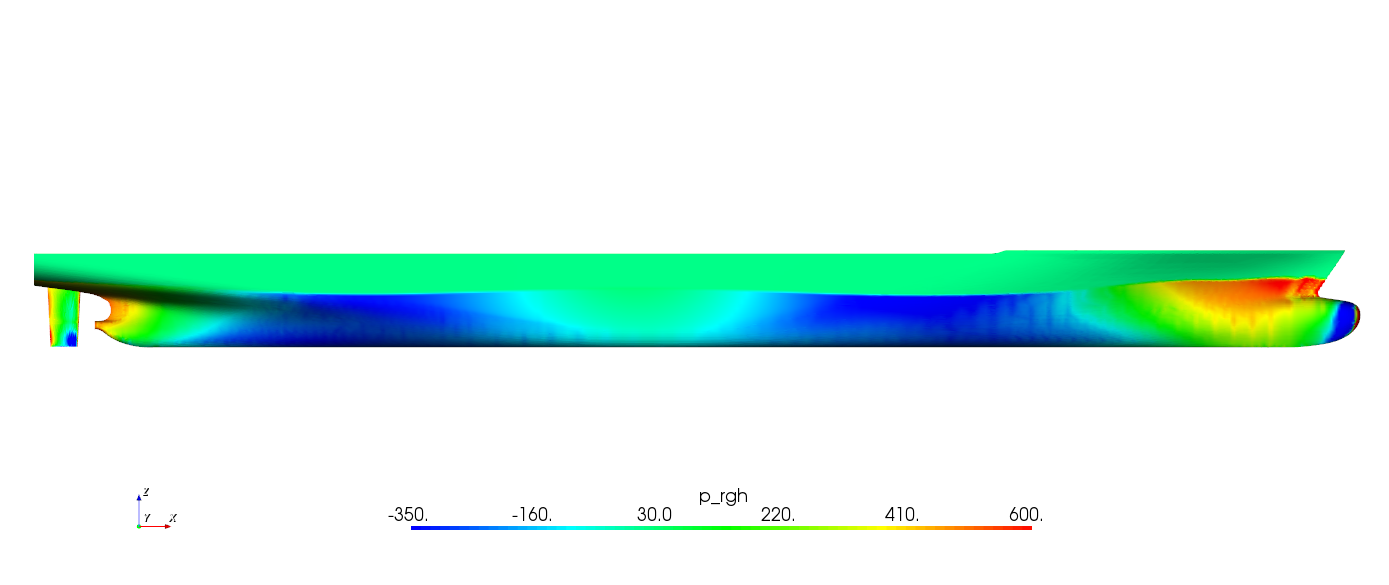
图2.13 船体表面压力分布云图
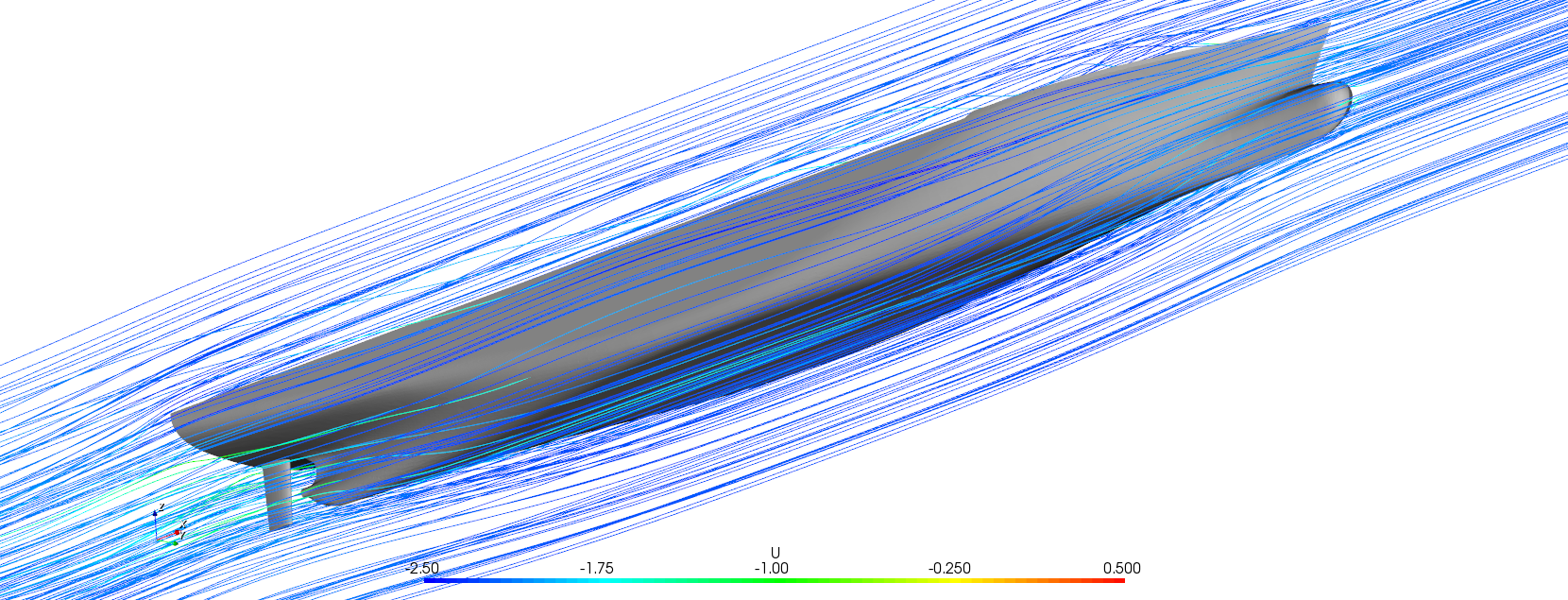
图2.14 船体周围流线
1.6 主流商业软件(starccm+)
1.6.1 计算网格

图2.15 starccm+商业软件计算网格
1.6.2 计算结果
| 速度(m/s) | 试验值(N) | 计算值(N) | 误差(%) |
|---|---|---|---|
| 2.196 | 85.48 | 83.8558 | -1.9 |
图2.16 船行波

图2.17 船体表面压力分布云图
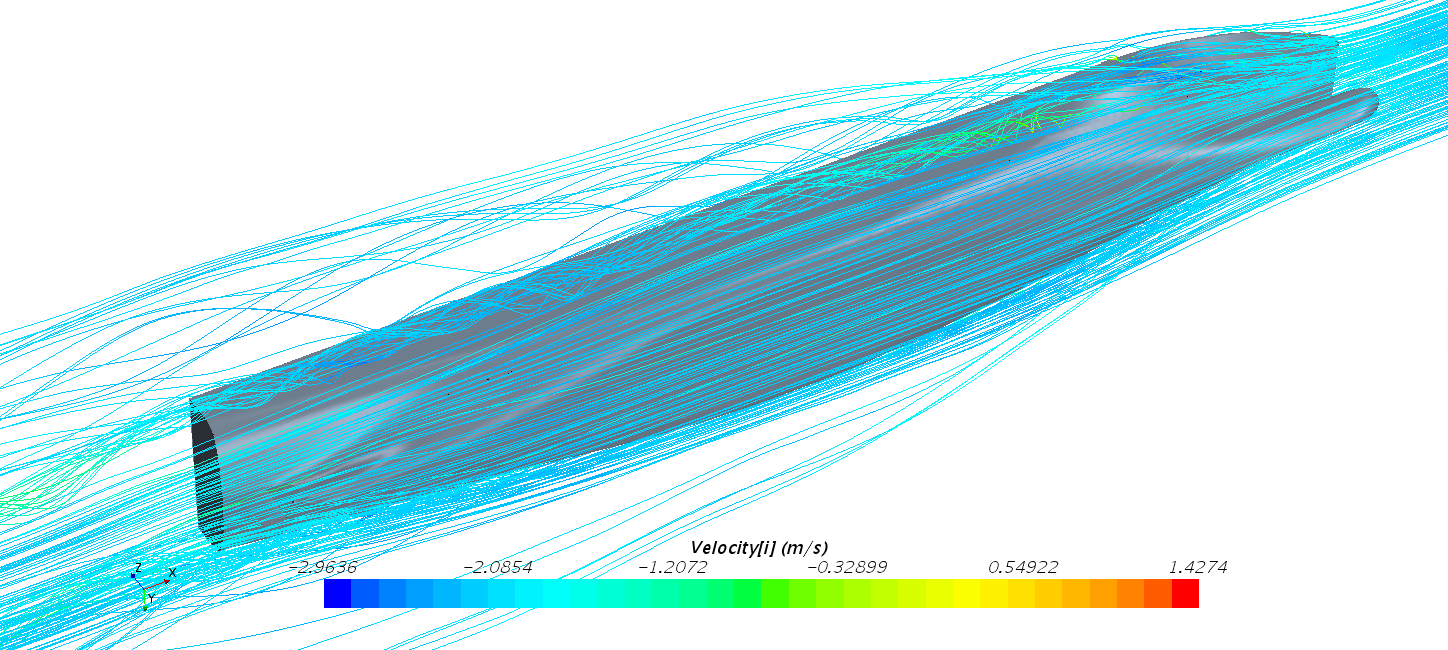
图2.18 船体周围流线
1.7 性能对比
选取KCS船作为计算对象,分别采用本虚拟试验与主流商业软件进行船模静水阻力计算,并就这两种工具进行了比对结果整理如下表:两个种方法均采用不可压缩的雷诺时均纳维—斯托克斯(Reynolds-Averaged Naiver-Stokes)方程作为控制方程,湍流模型选择为SST ;计算精度方面,两种方法的预报值与试验结果相比,计算精度相当,均在3%以内;耗时方面,本虚拟试验计算单个航速点的耗时为16个小时,商业软件Starccm+耗时较短为6.17个小时;另外,本虚拟试验中集成了专家知识库,可以一键实现网格划分及求解相关参数设置,操作简便,可以保证三大主力船型在设计航速点附近的计算精度。
| 对比项 | 虚拟试验 | Starccm+ |
|---|---|---|
| 计算方法 | RANS | RANS |
| 网格量(百万) | 2.08 | 1.58 |
| 精度(%) | -2.1 | -1.9 |
| 效率(耗时) | 16h(32核) | 6.17h(32核) |
| 专家策略 | 有 | 无 |
1.8 案例视频
1.9 工业应用
本虚拟试验邀请了广船国际有限公司和中船重工设计研究中心、大连船舶重工集团有限公司、中远海运重工、佳豪船舶设计公司等工业用户进行试用,分别针对油船、散货船和集装箱船进行计算,计算精度良好,取得了较好的评价。

图2.19 船行波




操作指南
开始试验1. 试验创建
当前虚拟试验提供两种试验创建的方法:通过样例创建试验和创建空白试验。
1.1 通过样例创建试验
进入船模阻力虚拟试验后,点击右侧任一一个样例试验,如图3.1所示。
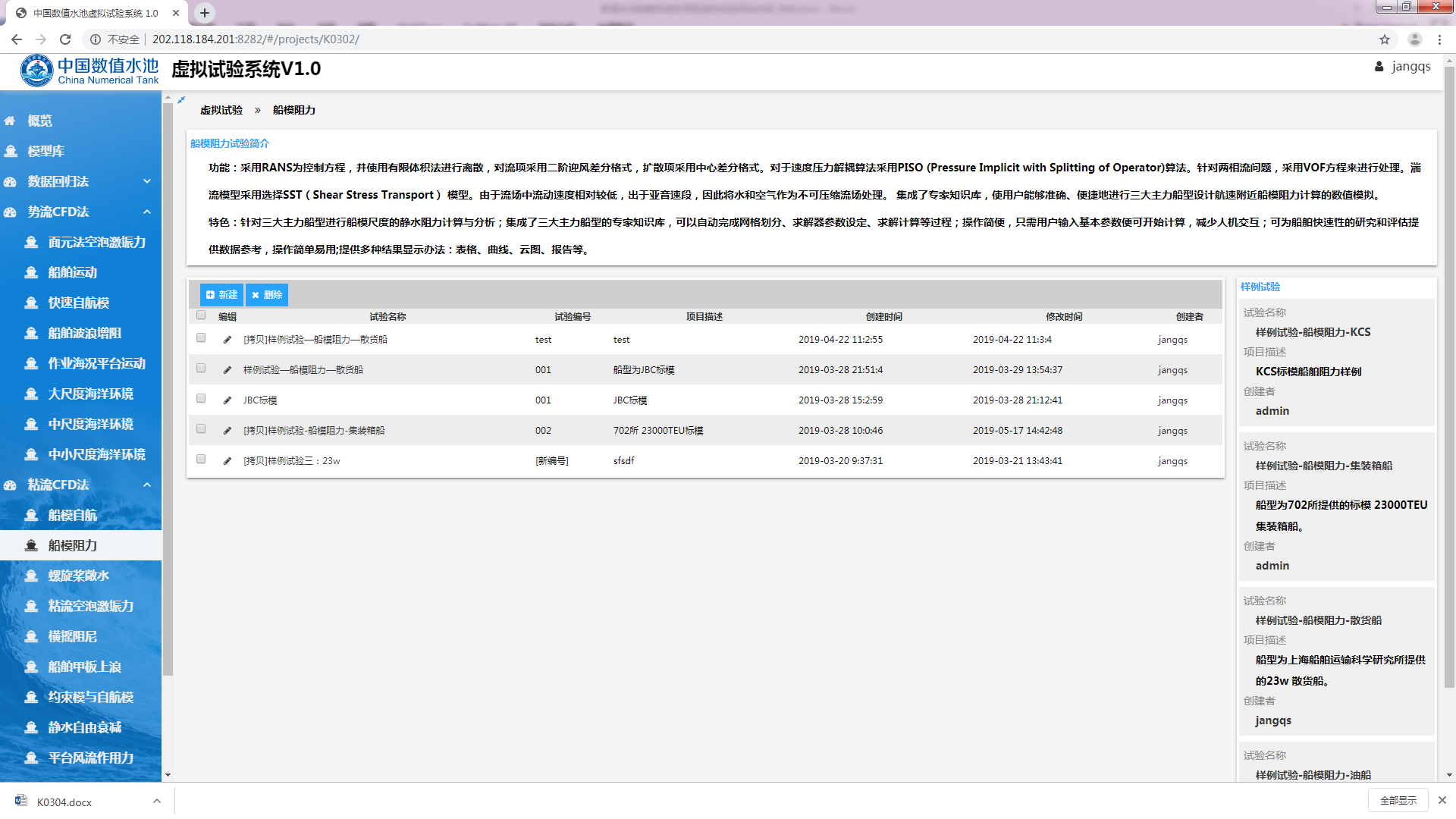
图3.1 船模阻力虚拟试验网页界面
进入某一样例试验后,鼠标移动至页面右上角 处,即可显示当前虚拟试验的相关信息,如图3.2所示。
处,即可显示当前虚拟试验的相关信息,如图3.2所示。
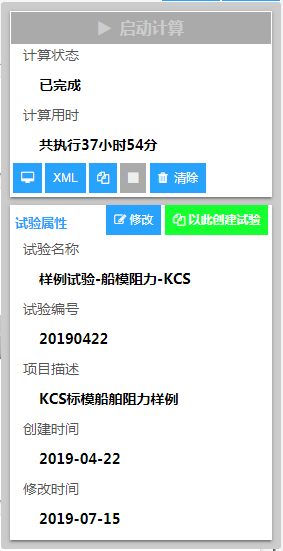
图3.2 样例试验属性
点击图3.2中的绿色按钮“以此创建试验”,网页上会弹出新的对话框,提示用户输入新建试验的相关信息,如图3.3所示。通过这种方式创建的新试验是样例试验的一个拷贝,其参数与样例试验相同,用户只需按实际情况修改部分参数即可。因此,可将样例试验看成试验模板,起到初始化试验参数的作用,推荐通过该方法创建新试验,如图3.4。
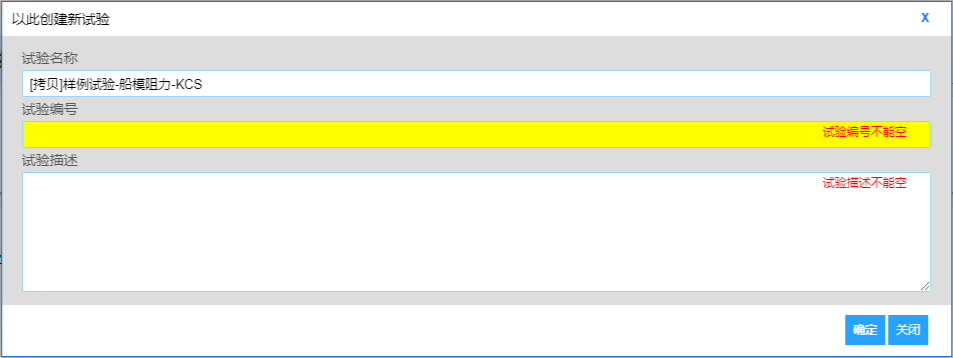
图3.3 基于样例创建新试验
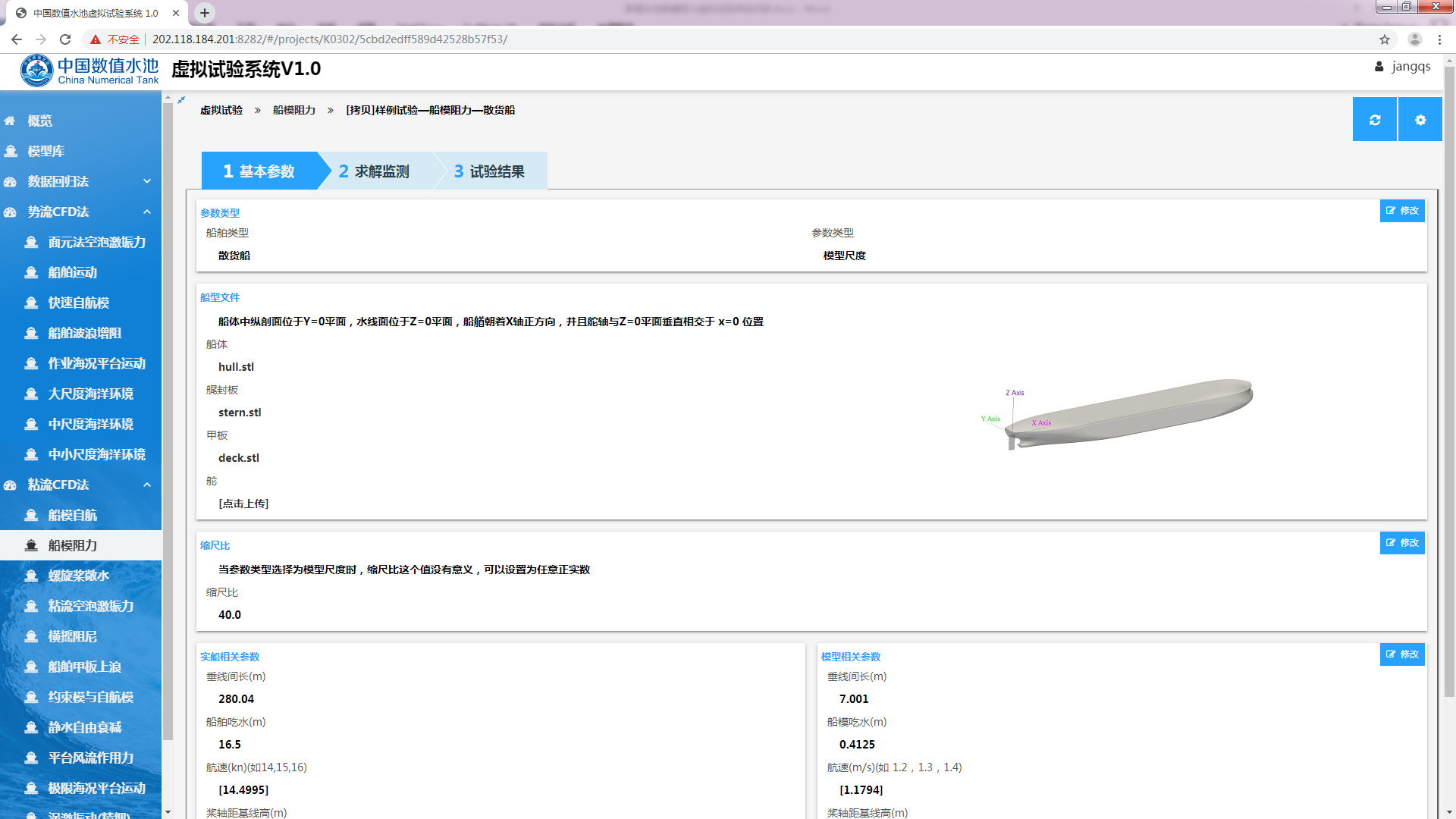
图3.4 基于样例创建的新试验
1.2 创建空白试验
进入船模阻力虚拟试验后,在该虚拟试验简介的下方找到蓝色“新建”按钮,如图3.5所示。
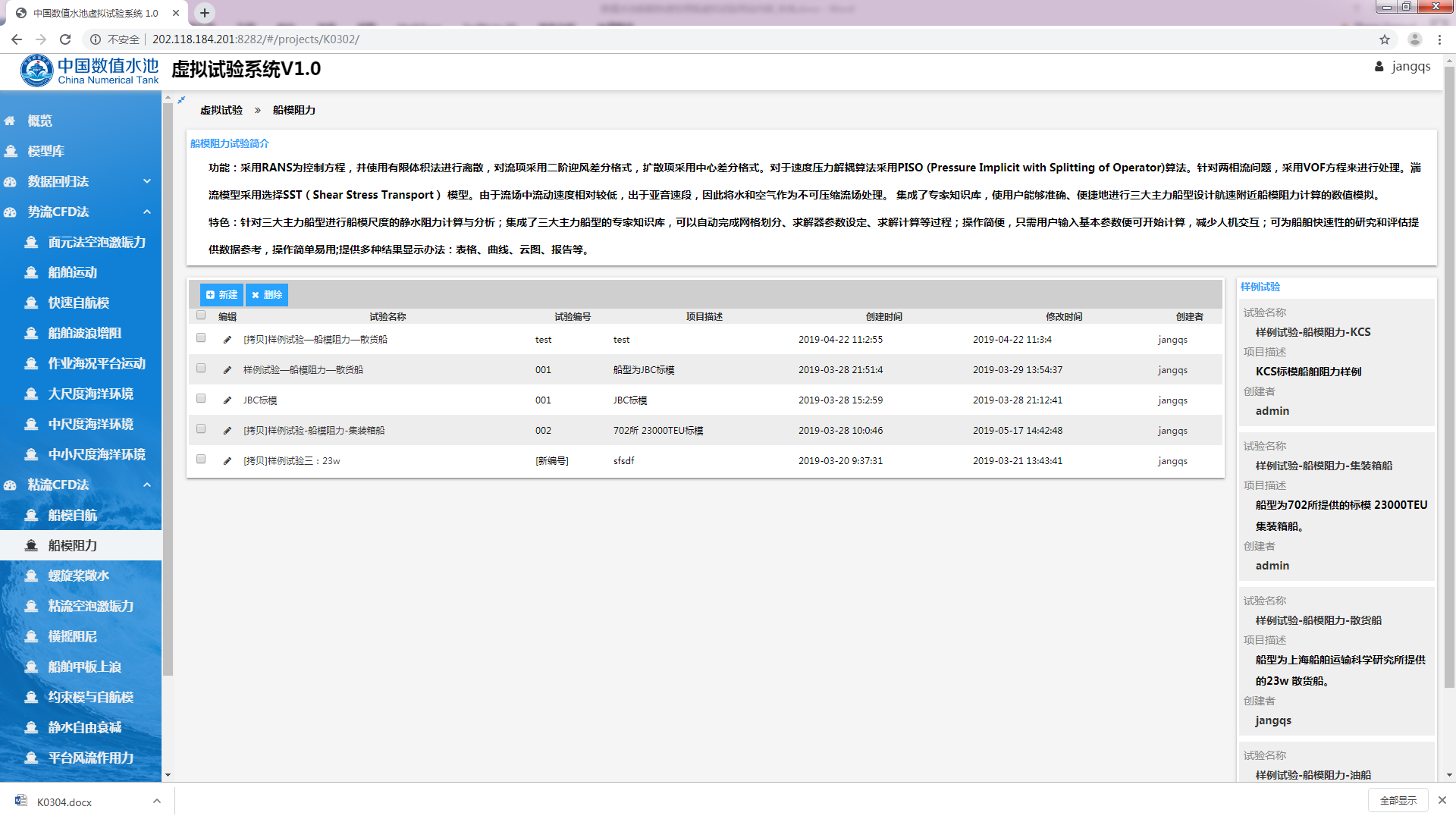
图3.5 船模阻力虚拟试验界面
点击“新建”按钮之后,会弹出一个对话框,在其中填入相应的必填信息后,点击“确定”即可创建一个新的空白试验。新建空白试验后,会自动跳转到该试验的详情页面,如图3.6所示。可见通过这种方法创建的虚拟试验中所有的参数都是空白的,用户需要手动输入相应的参数,方可进行计算,该方法适用于一定经验的用户。
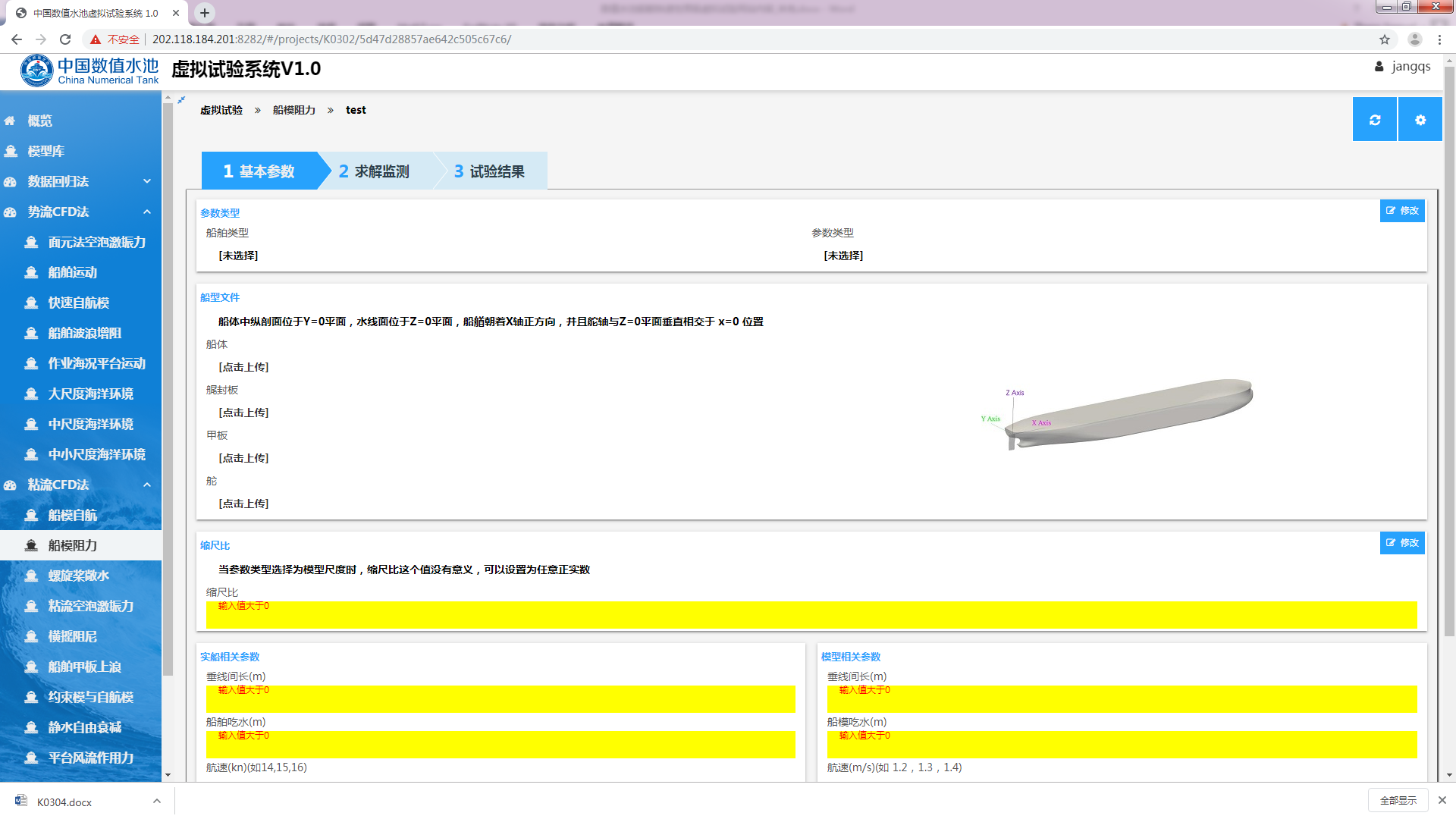
图3.6 空白试验详情页面
2. 参数录入
新的虚拟试验创建后,用户需要根据实际情况修改或录入船型相关参数,并确认所录入的参数符合实际情况。点击页面中的“基本参数”标签,即可进入参数设置页面,如图3.7所示。
其中,“船型文件”的船体、甲板、艉封板、舵分别为船体各个部位的几何文件,需要用户自行上传,支持stl格式。需要注意的是,上传的几何需保证坐标系:坐标原点为中纵剖面、水线面及0站横剖面的交点,船艏朝X轴正方向。
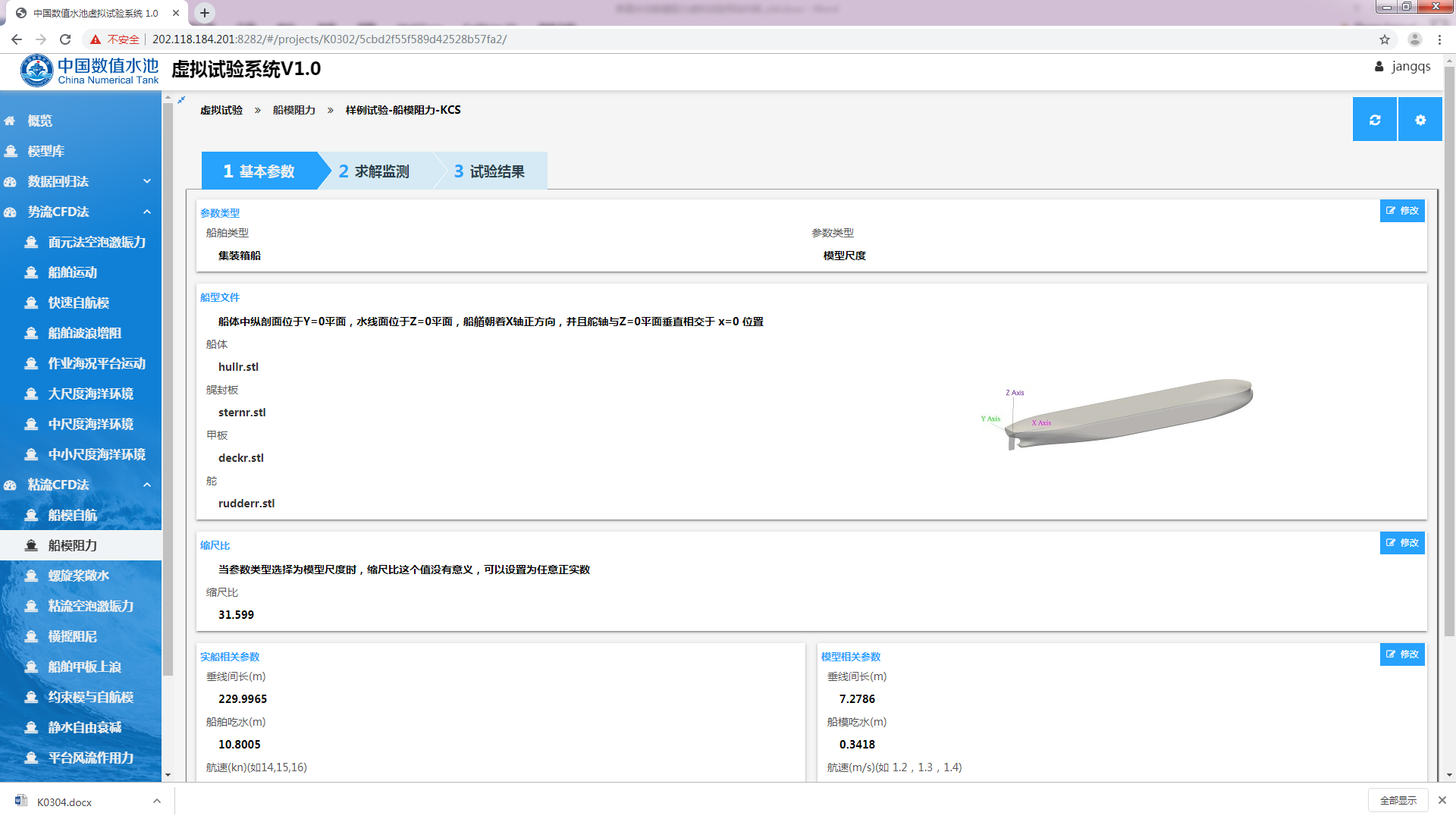
图3.7 “基本参数”页面
点击页面中的“点击上传”按钮,即弹出如图3.8所示的页面,用户需在此上传船体相关几何部件。其他船体几何部件,用户可采用类似的操作进行上传。
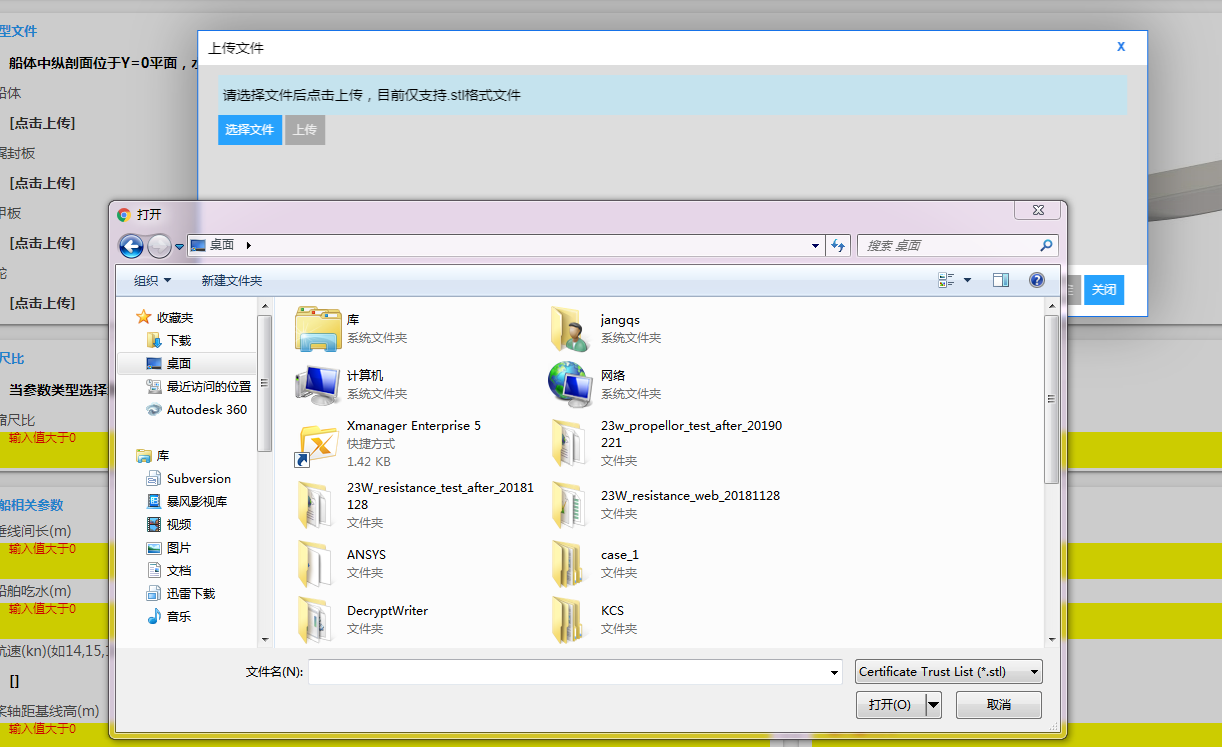
图3.8 上传船体几何相关文件
其他基本参数根据实际情况进行填写,特别需要注意的是,用户上传的几何文件及填写的船型相关数据需与参数类型中的选择一致,即上传实尺度几何文件,填写实尺度船型数据;或者上传模型尺度几何文件,填写模型尺度船型数据。避免船型参数与几何文件不对应造成计算错乱或计算结果不真实的现象。
3. 计算求解
3.1 启动计算
全部参数正确设置后,可启动求解器进行计算,如图3.9所,鼠标移动至右上角  处,页面会自动弹出当前虚拟试验的试验属性,点击其中的橙色“启动计算”按钮即可开始计算。
处,页面会自动弹出当前虚拟试验的试验属性,点击其中的橙色“启动计算”按钮即可开始计算。
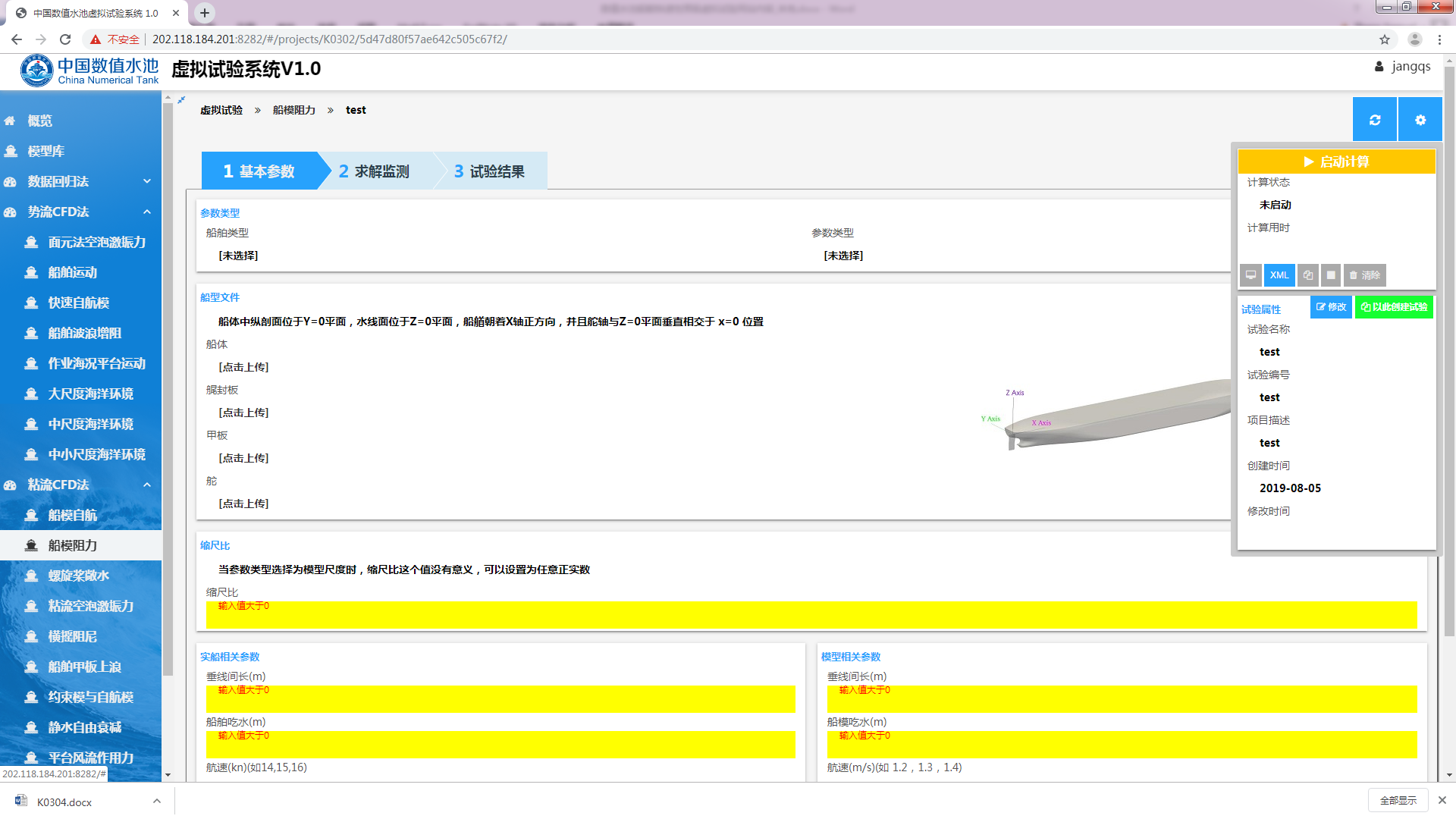
图3.9 试验属性页面
点击“启动计算”后,页面会弹出启动求解器的对话框,如图3.10所示,用户点击“确定”以继续。

图3.10 求解器启动确认对话框
3.2 过程监测
计算启动,用户可以通过“求解监测”标签来实时的查看当前虚拟试验的计算状态,如显示单个航速下的残差曲线(图3.11)、单个航速下的阻力曲线(图3.12)、多个航速下的阻力曲线(图3.13)。
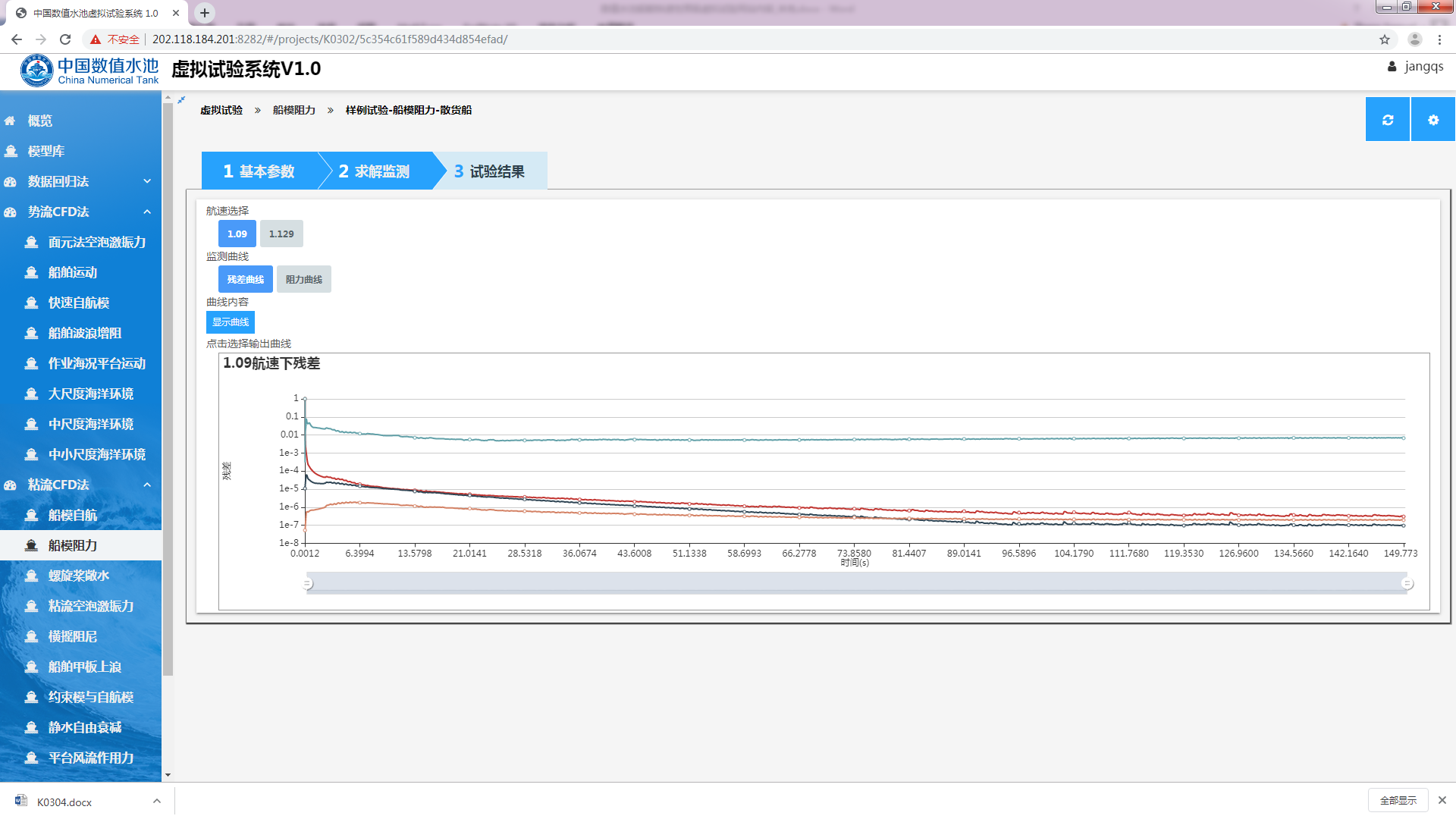
图3.11 单个航速下的残差曲线
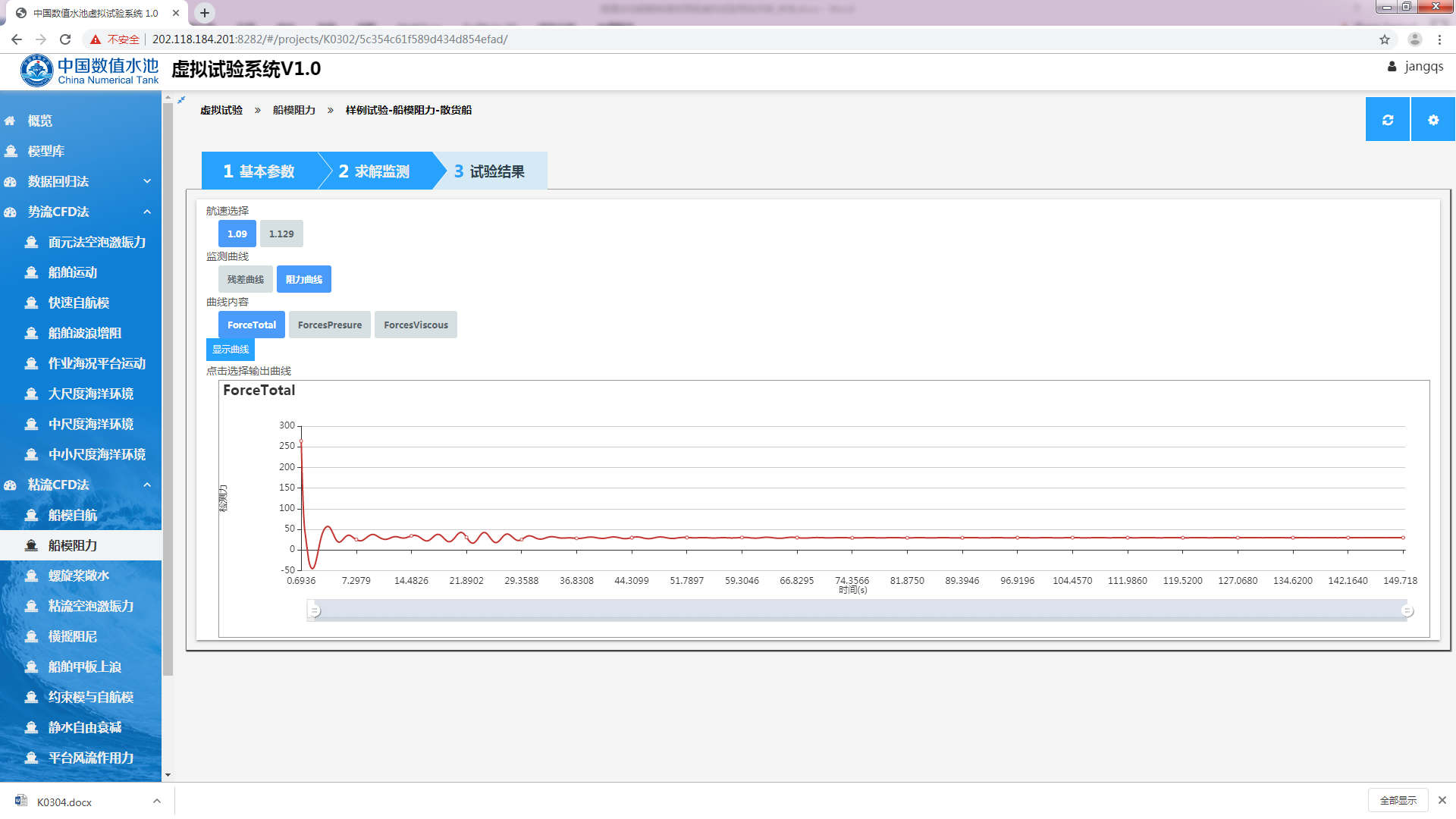
图3.12 单个航速下的阻力曲线
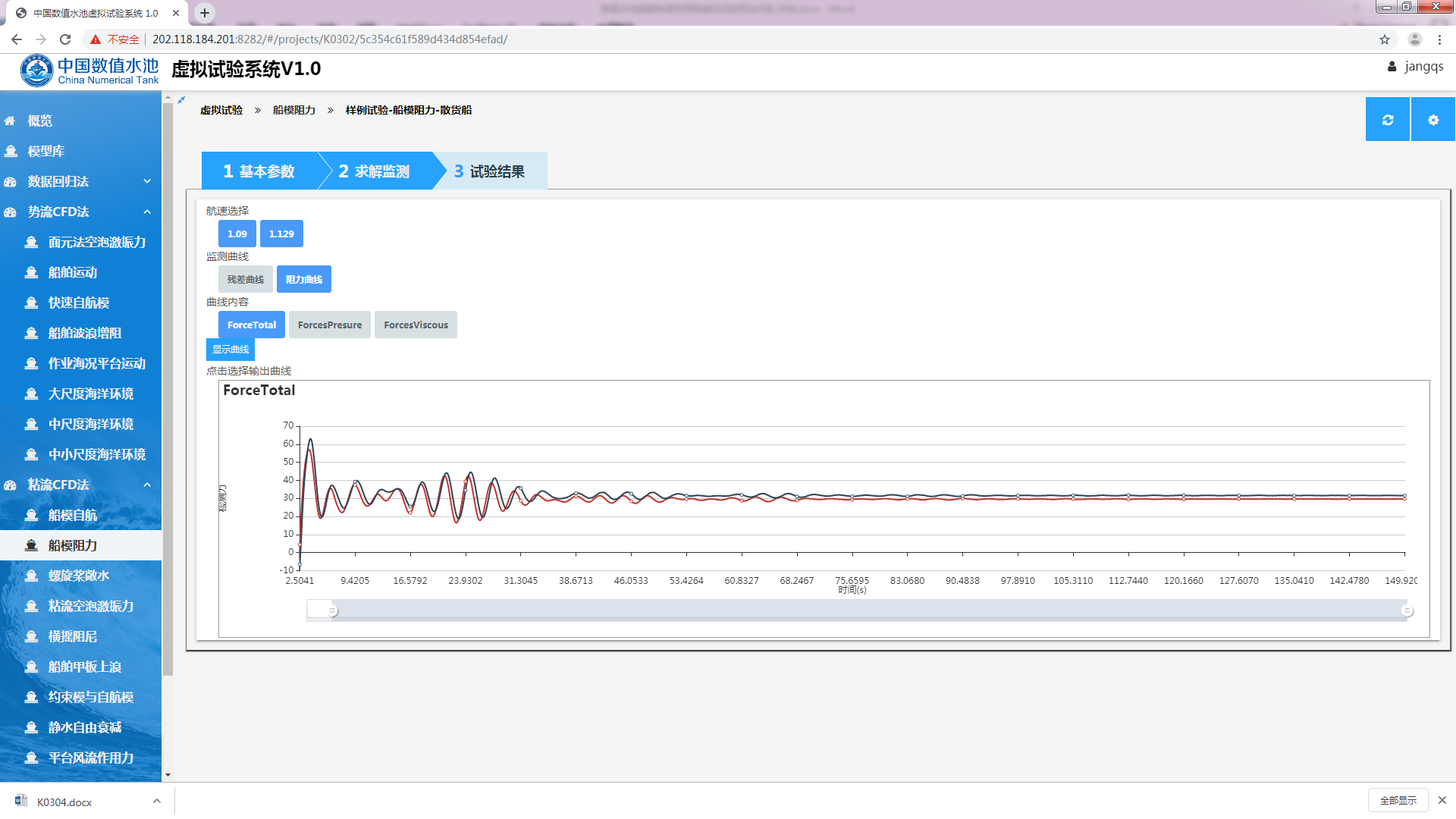
图3.13 多个航速下的阻力曲线
4. 结果显示
计算结束后,用户可切换到“试验结果”标签中来查看当前虚拟试验的计算结果。用户可以点击右上角的试验报告按钮,下载当前虚拟试验的结果报告,如图3.14所示。

图3.14 试验报告展示
用户同样可以选择在线浏览计算结果,在“试验结果”标签下的选择不同的航速来,网页会自而动刷新以展示相应的内容,如图3.15~17所示。
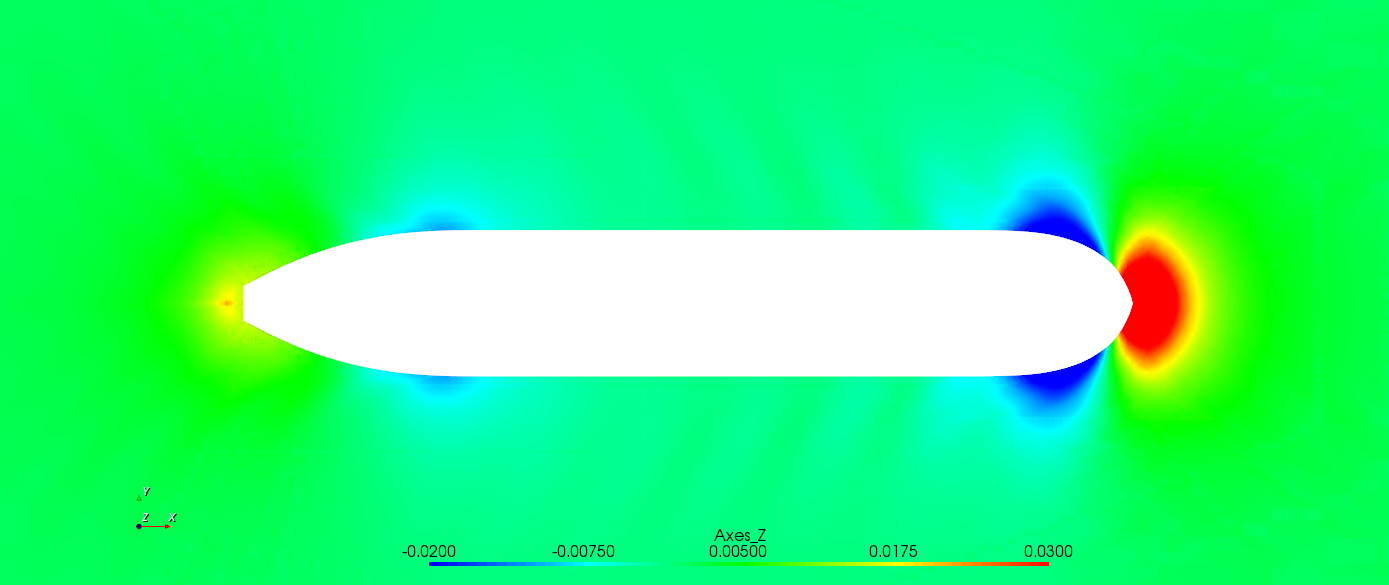
图3.15 船行波
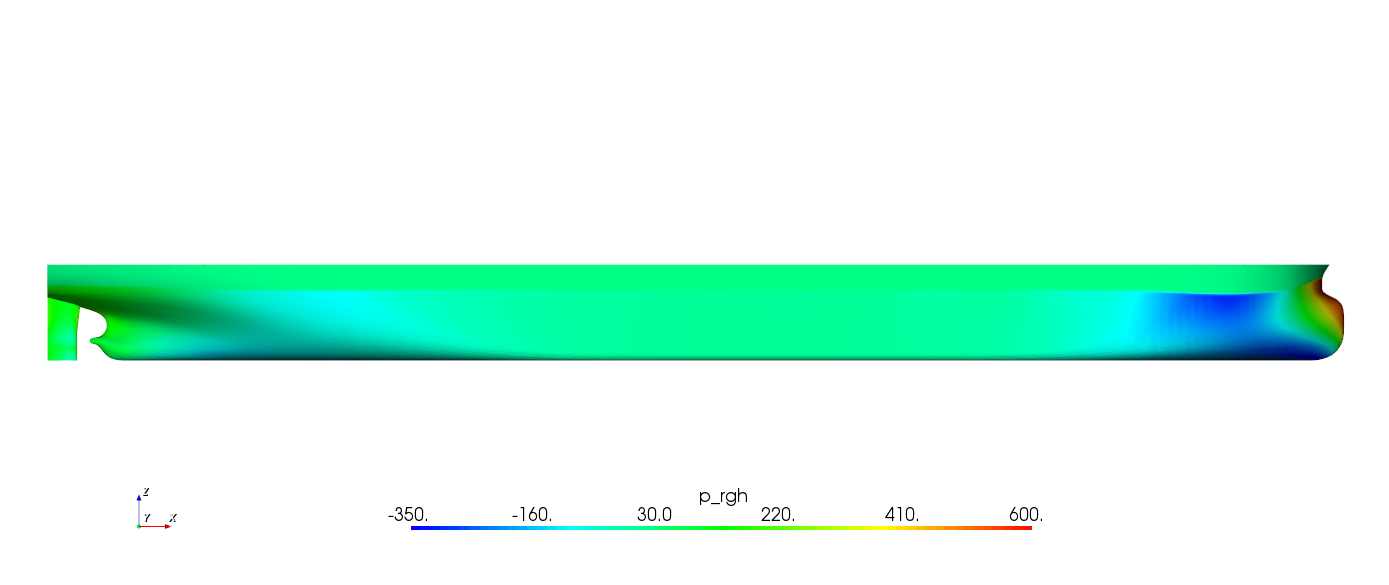
图3.16 船体表面压力分布
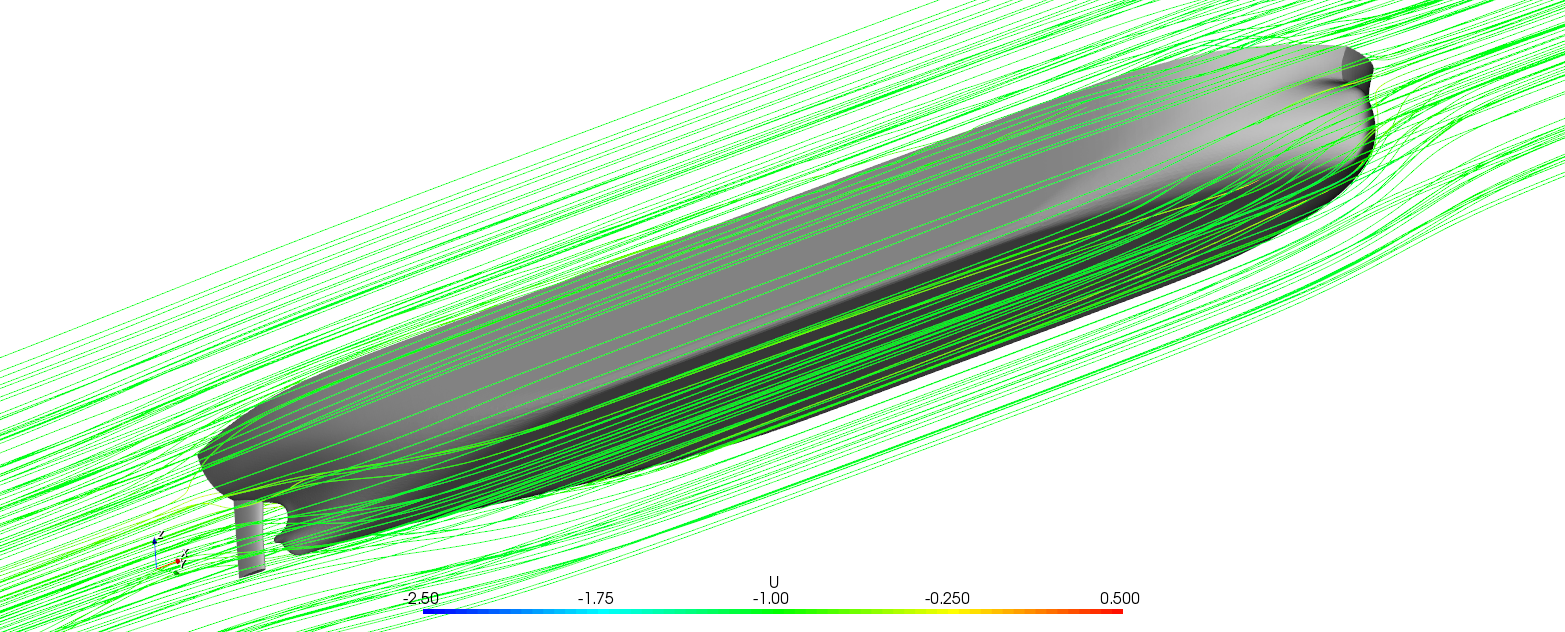
图3.17 船体周围流线
参考资料
开始试验1. 参考文献
[1] Versteeg H.K., Malalasekera W. An introduction to computational fluid dynamics: The finite volume method. Wiley, New York, 1995.
[2] Bradshaw P., Cebeci T., Whitelaw J.H. Engineering calculation methods for turbulent flow [M], Academic Press, London, 1981.
[3] Patankar, S., Algorithm for assembling overlapping grid system [J], Hemisphere Pub, 1980.
[4] Van Doormaal, J., Raithby, G., Enhancements of the SIMPLE method for predicting incompressible fluid flows [J], Numerical Heat Transfer, 1984, 7:147-163.
[5] Ubbink, O., Issa, R.I., A Method for Capturing Sharp Fluid Interfaces on Arbitrary Meshes [J], Journal of Computational Physics. 1999, 153(1): 26 – 50.
[6] Rusche, H. Computational fluid dynamics of dispersed two-phase flows at high phase fractions [Dissertation]. London, UK, Imperial College, 2002.
[7] Berberović, E., van Hinsberg, N., Jakirlić, S., et al. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution [J]. Physical Review E. 2009, 79(3): 36306.
[8] 马娟,水面船舶和高性能多体船兴波与阻力性能计算 [D],上海:上海交通大学,2011.
[9] Menter, F.R., Kuntz, M., Langtry, R. Ten years of industrial experience with the SST turbulence model[J]. Turbulence, heat and mass transfer. 2003, 4: 625–632.
[10] Wilcox, D.C. Turbulence modeling for CFD [M]. 3rd Edition. La Canada, CA, DCW industries, 2006.
[11] Jones, W.P., Launder, B.E. The prediction of laminarization with a two-equation model of turbulence[J]. International Journal of Heat and Mass Transfer. 1972, 15(2):301–314.
[12] Bredberg, J. On the Wall Boundary Condition for Turbulence Models[R]. Internal Report 00/4, Gothenburg, Sweden, Chalmers University of Technology, 2000.
[13] Menter, F., Carregal Ferreira, J., Esch, T., et al. The SST Turbulence Model with Improved Wall Treatment for Heat Transfer Predictions in Gas Turbines[C]. In the Proceedings of the International Gas Turbine Congress. Tokyo, Japan, 2003.
[14] Wilcox, D.C. Turbulence modeling for CFD [M]. 3rd Edition. La Canada, CA, DCW industries, 2006.
2. 研究团队
1. 上海船舶运输科学研究所航运技术与安全中心董国祥;
2. 上海船舶运输科学研究所航运技术与安全中心陈伟民
3. 上海船舶运输科学研究所航运技术与安全中心张青山;
4. 上海船舶运输科学研究所航运技术与安全中心杨 帆;
5. 上海船舶运输科学研究所航运技术与安全中心陈昆鹏;
6. 上海船舶运输科学研究所航运技术与安全中心任海奎;
7. 上海船舶运输科学研究所航运技术与安全中心车霖源;
8. 上海船舶运输科学研究所航运技术与安全中心杜云龙;
3. 研究进展
1. 2016.12,船舶快速性计算理论对比及算法研究;
2. 2017.12,船模阻力计算软件的开发;
3. 2018.06,船模阻力计算策略开发完成;
4. 2018.07,船模阻力专家知识库的开发与集成;
5. 2018.10,船模阻力计算策略更新,同时更新专家知识库;
6. 2018.11,船模阻力计算策略更新,同时更新专家知识库;
7. 2018.11,第一次用户咨询会;
8. 2019.07,第二次用户咨询会;
4. 实用工具
C++、QT;
咨询电话:0451-82569306
版权所有:数值水池 信息维护:数值水池创新团队 地址:哈尔滨市南岗区南通大街145号 邮编:150001
联系我们:nwt@hrbeu.edu.cn;zhaobin2_1984@163.com 黑ICP备17002841号-10 公安备案号:23010302000541










