您当前位置:试验中心 >浏览文章
船舶摇荡运动虚拟试验
Wave Induced Ship Motions Virtual Test System试验介绍
开始试验1.功能介绍
本系统基于三维时域势流脉冲响应函数理论开发,运用匹配法思想构造流体运动的边界积分方程,利用独创的泰勒展开边界元方法求解。可进行船舶三维水波辐射和绕射水动力虚拟试验,进行全浪向规则波和不规则波船舶摇荡运动虚拟试验,也可进行不规则波中船舶上浪、砰击和螺旋桨出水概率虚拟试验。
主要功能有:
(1)全浪向规则波下船舶摇荡运动虚拟试验;
(2)全浪向不规则波船舶摇荡运动虚拟试验;
(3)不规则波中船舶上浪、砰击和螺旋桨出水概率统计虚拟试验。
2.产品特色
(1)核心求解器采用独创的泰勒展开边界元法,求解效率高;
(2)网格可自动生成;
(3)实现全浪向模拟,可对上浪、砰击和螺旋桨出水概率进行计算;
(4)试验结果展示:时历和响应曲线,谱分析表格,可生成报告。
3.运行环境和效率
本虚拟试验系统基于势流理论方法开发,单机版对计算机要求较低,在主流PC机,Windows系统上即可运行。基于Openmp开展并行计算,需要配置Openmp库环境。
4.试验精度
在五级海况下相对于船模试验垂荡、纵摇和横摇运动有义值误差在15%以内。
典型案例
开始试验(一)案例一 14000TEU集装箱船迎浪下的摇荡运动虚拟试验
1.1 案例名称
案例试验- 14000TEU集装箱船迎浪下的摇荡运动虚拟试验
1.2 案例描述
本案例针对某14000TEU集装箱船展开船舶摇荡运动虚拟试验。航速分别为12节,浪向180°。通过CNT-TEBEM-WIM软件对划分好的网格进行计算,在设置时间步,圆频率、航速等参数后进行虚拟试验,得到垂荡和纵摇运动响应曲线。虚拟试验结果与模型试验吻合度较好。
1.3 性能比对
计算结果对比如下图2.1
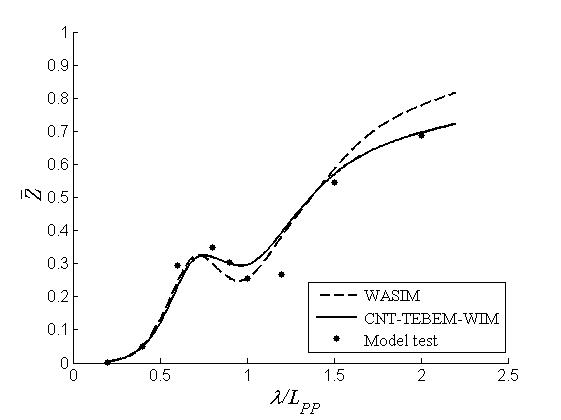

(a) 垂荡对比
(b) 纵摇对比
图2.1 集装箱船运动计算结果对比
通过上面的对比可以看出,两种软件计算精度相当,能够给出同一精度水平的预报结果。
1.4 工业应用
在中国船级社用于第二代船舶动稳性评估研究,效果良好。
(二)案例一 育鹏号船斜浪下的摇荡运动虚拟试验
1.1 案例名称
案例试验- 14000TEU集装箱船迎浪下的摇荡运动虚拟试验
1.2 案例描述
本案例针对育鹏号船展开斜浪中的船舶摇荡运动虚拟试验。航速为0节,浪向135°。通过CNT-TEBEM-WIM软件对划分好的网格进行计算,在设置时间步,圆频率、航速等参数后进行虚拟试验,得到垂荡和纵摇运动响应曲线。本软件可以很好模拟斜浪中的摇荡运动,虚拟试验结果与模型试验吻合度较好。
1.3 性能比对
结果对比如下图2.2所示
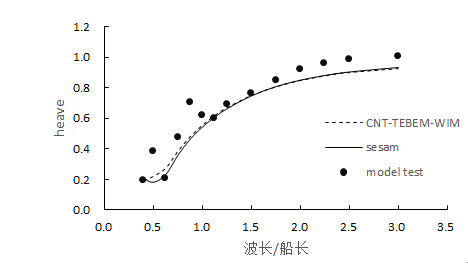
(a) 垂荡对比
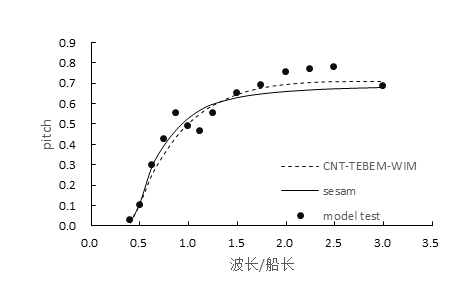
(b) 纵摇对比
图2.2 育鹏号结果对比
(三)案例一 阿芙拉油船顶浪下的摇荡运动虚拟试验
1.1 案例名称
案例试验- 阿芙拉油船顶浪下的摇荡运动虚拟试验
1.2 案例描述
案例针对阿芙拉油船展开斜浪中的船舶摇荡运动虚拟试验。航速为12节,浪向分别为顶浪180°、顶斜浪135°。通过CNT-TEBEM-WIM软件对划分好的网格进行计算,在设置时间步,圆频率、航速等参数后进行虚拟试验,得到垂荡和纵摇运动响应曲线。虚拟试验结果与模型试验吻合度较好。
1.3 性能比对

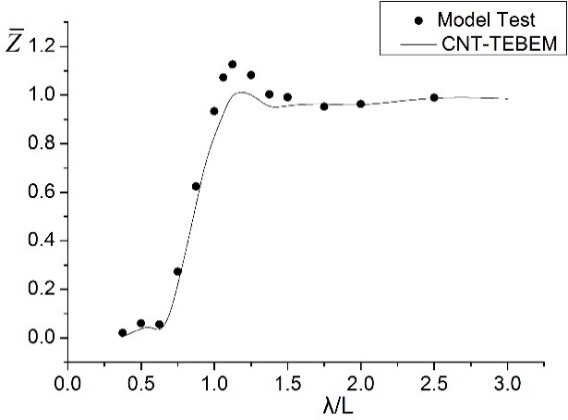
(a) 180°垂荡对比
(b) 135°垂荡对比
图2.1 集装箱船运动计算结果对比
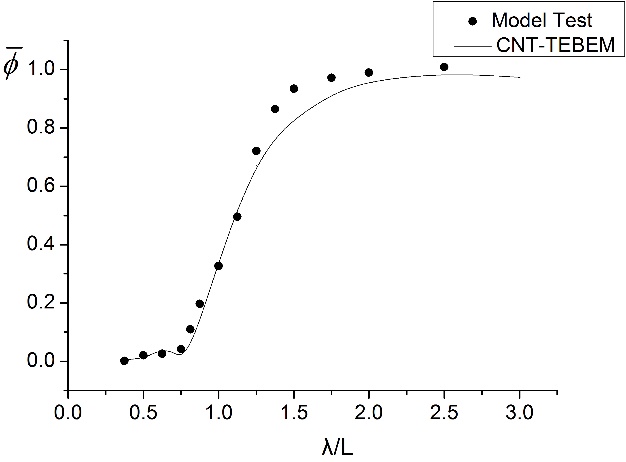
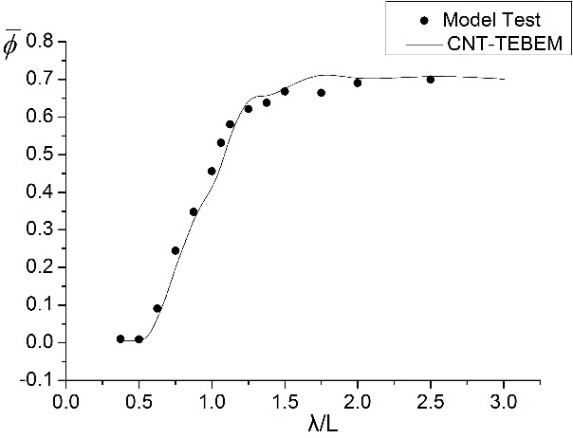
(c) 180°纵摇对比
(d) 135°纵摇对比
图2.3 阿芙拉油船结果对比
操作指南
开始试验用户登录中国数值水池虚拟试验系统后,可完成系统提供的各类虚拟试验。虽然试验在参数、求解器、计算结果等方面区别很大,但总体上来说操作过程基本相同,主要由四个部分组成:1试验创建;2参数录入(前处理);3计算求解;4结果展示(后处理)。
登录系统后,点击页面左侧导航栏中的“船舶运动”,从而进入该试验的管理页面。如下图所示,该页面有关于极限海况的主要功能介绍,以及该虚拟试验的相关特色。
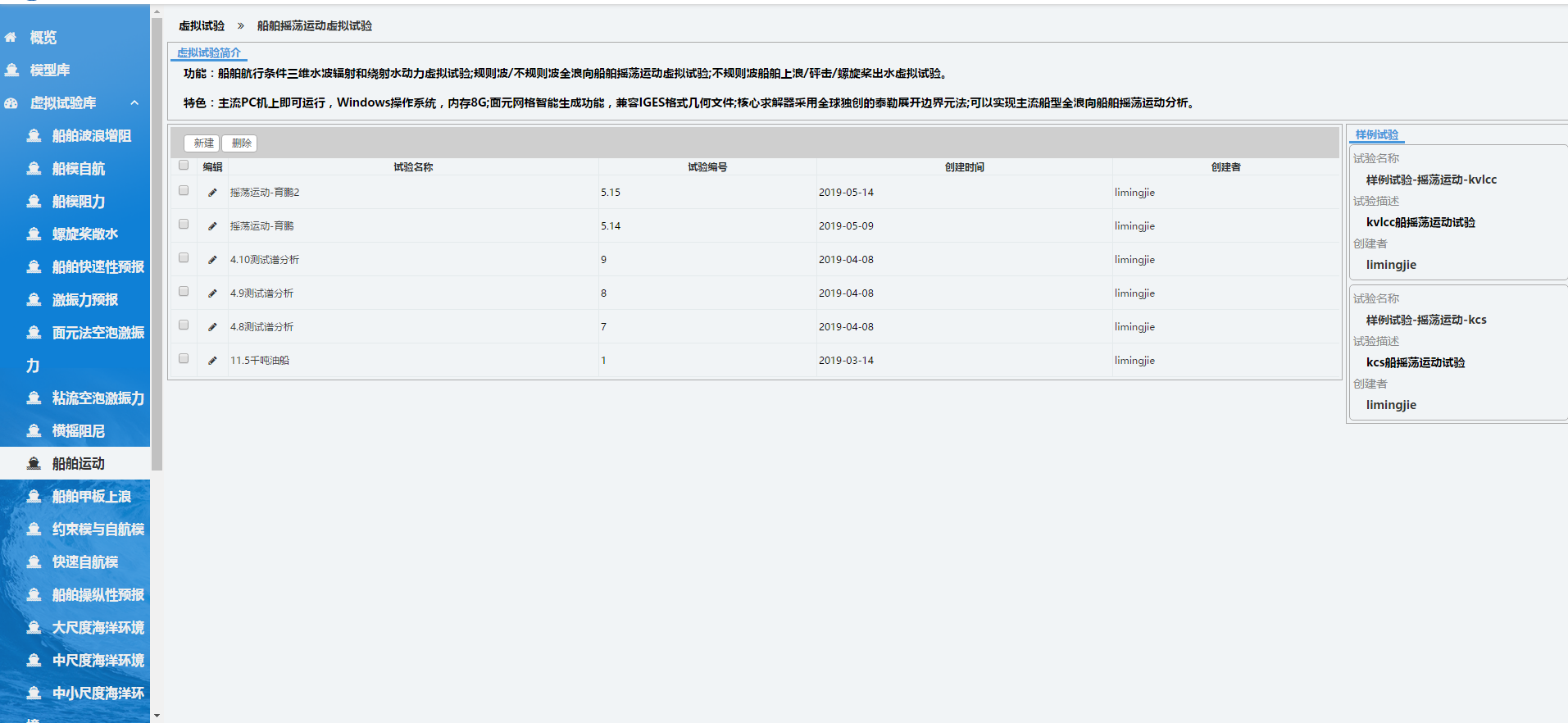
下面给出用户做过的试验列表,该列表以时间顺序排序,可以在看到用户做的每一个虚拟试验的概要信息,如试验名称、编号、描述、创建时间、修改时间等内容,用户可在这里对试验进行创建核删除操作。
页面的右侧是船舶运动的“样例试验”,如下图所示。样例试验是系统提供的已经完成的试验,对系统中的所有注册用户开放,可给用户提供一定的参考,从而更好地完成自己的虚拟试验。点击“样例试验”后,则进入样例试验的详情界面,可以看到样例试验的参数设置、求解器的执行信息及试验的结果。这里,用户可以查看样例的所有信息,但不可以修改。

1.试验创建
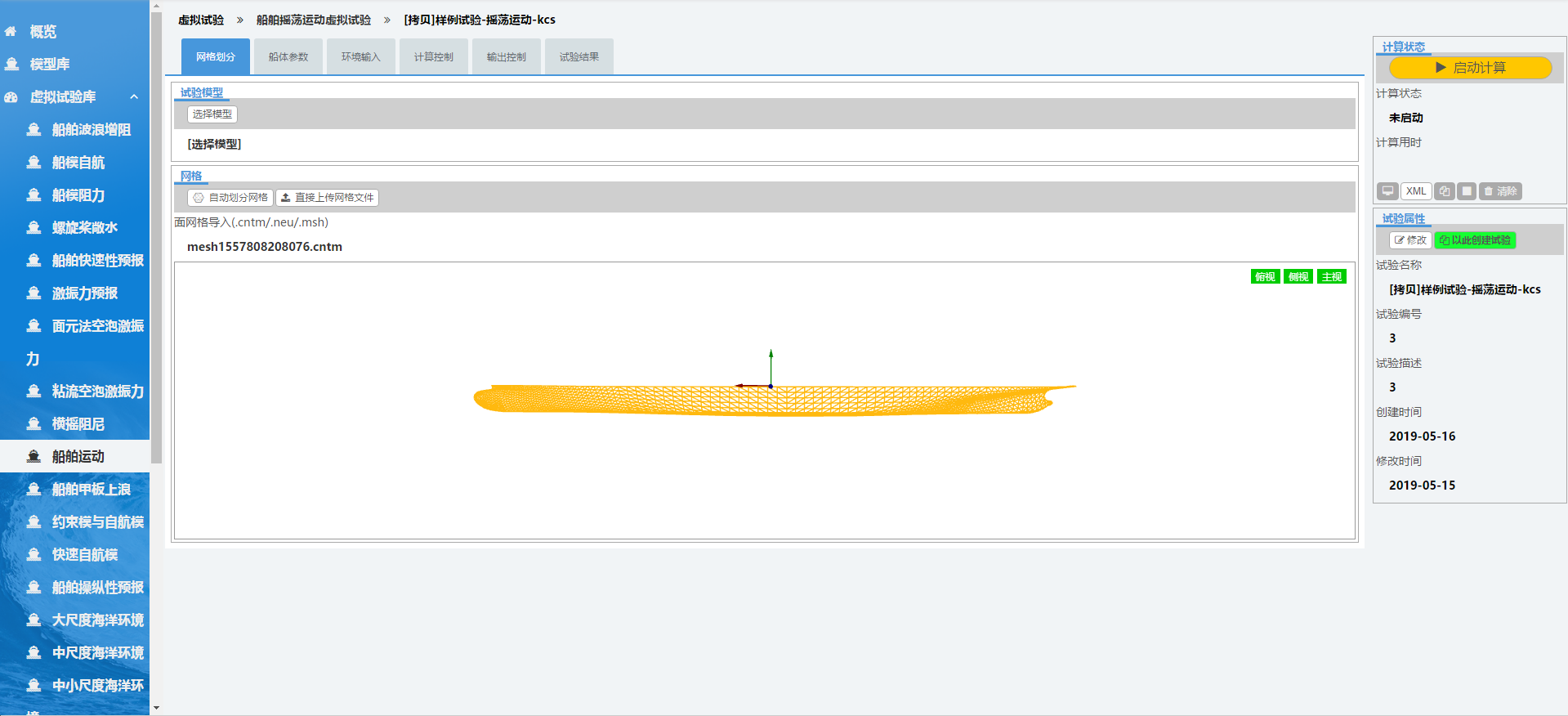
系统提供了两种创建虚拟试验的方法,第一种是通过某个虚拟试验为范本来创建虚拟试验。如下图所示,点开某个虚拟试验的详情页面,在这个页面的右侧 “以此创建试验”,则弹出创建新试验的对话框,输入适当的试验名称、编号及描述,点击确定即可完成新试验的创建。
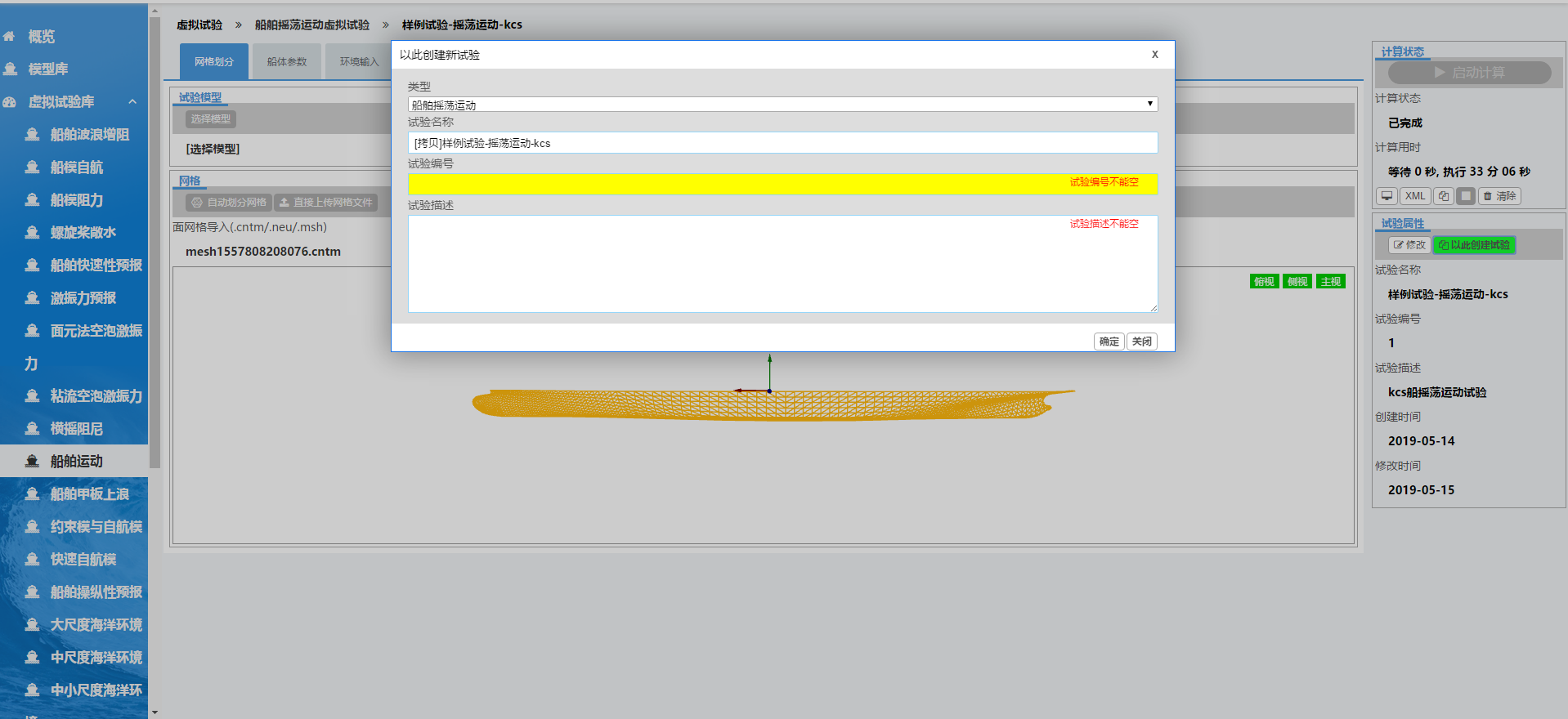
如下图所示,新试验创建后将自动跳转到该试验的详情页面,可见通过这种方式创建的新试验是样例试验的一个拷贝,其参数与样例试验相同,用户只需按实际情况修改部分参数即可。因此,可将当前虚拟试验看成试验模板,起到初始化设定新试验参数的作用,系统推荐通过这样的方式来创建新的虚拟试验。
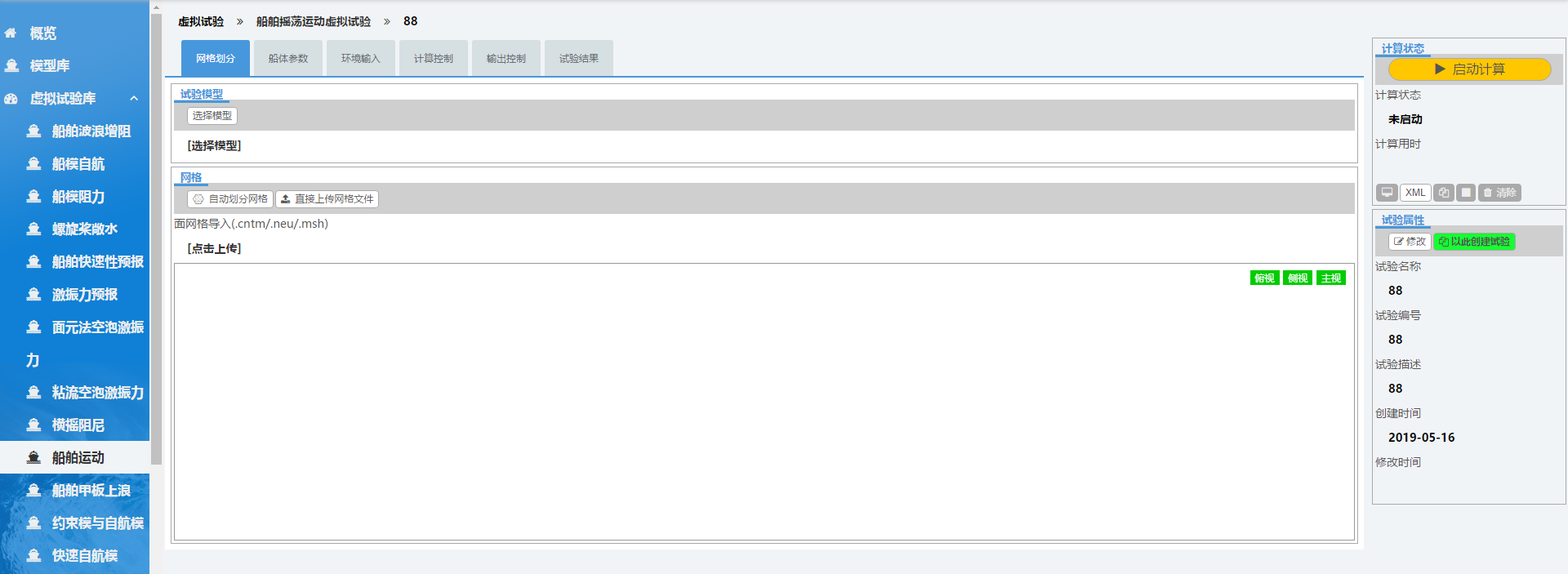
第二种创建新试验的方法是创建一个空白试验。如下图所示,通过点击“船舶运动”中虚拟试验列表上方的“新建”按钮,同样会弹出对话框如下图。填入相应的信息,然后点击确定,即可创建一个新的空白试验。.2所示。

如下图所示,新空白试验创建后,同样会自动跳转到该虚拟试验的详情页面。可见通过该方法创建的所有虚拟试验都是空白,需要用户手动输入所有的必填参数,方可进行计算,该方法适用于有一定经验的用户。
2. 参数录入
当一个新的虚拟试验创建口,用户需要对其参数进行适当的录入或修改,为确保结果的准确,请确认所录入的参数符合实际情况。
2.1 网格划分
在“网格划分”标签中,可以选择模型,点击“自动网格划分”。也可点击“直接上传网格”按钮,可进入如下图所示页面,可以进行网格上传的设置。
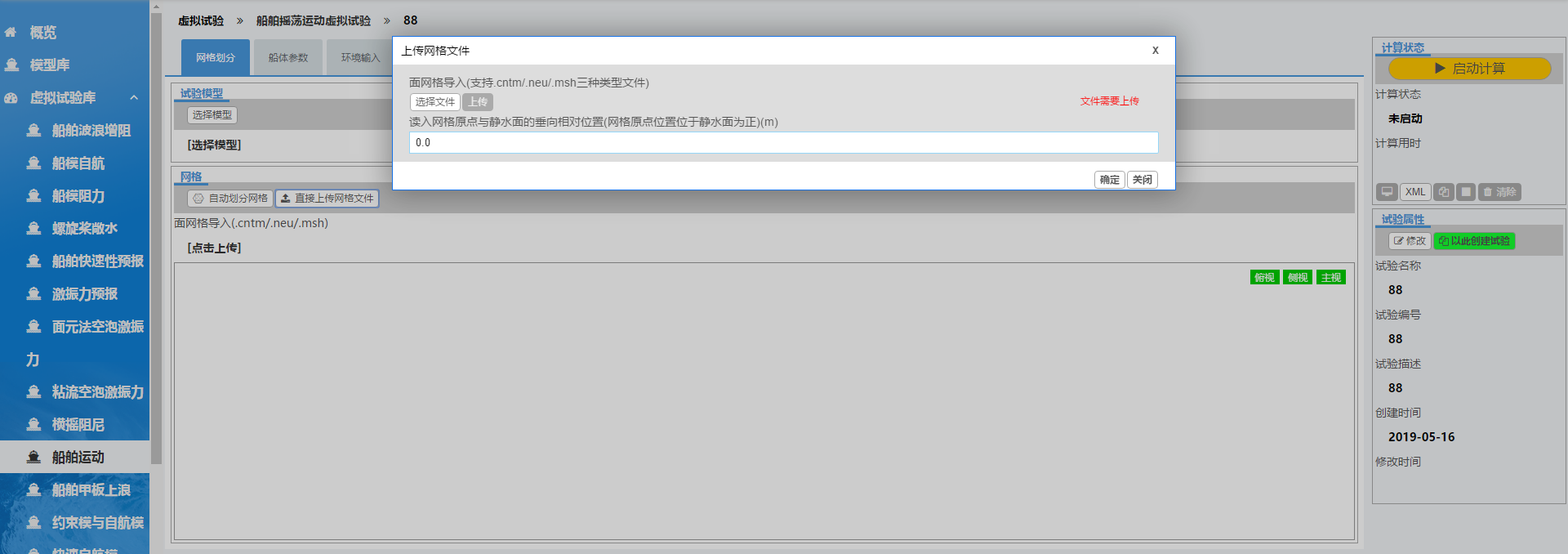
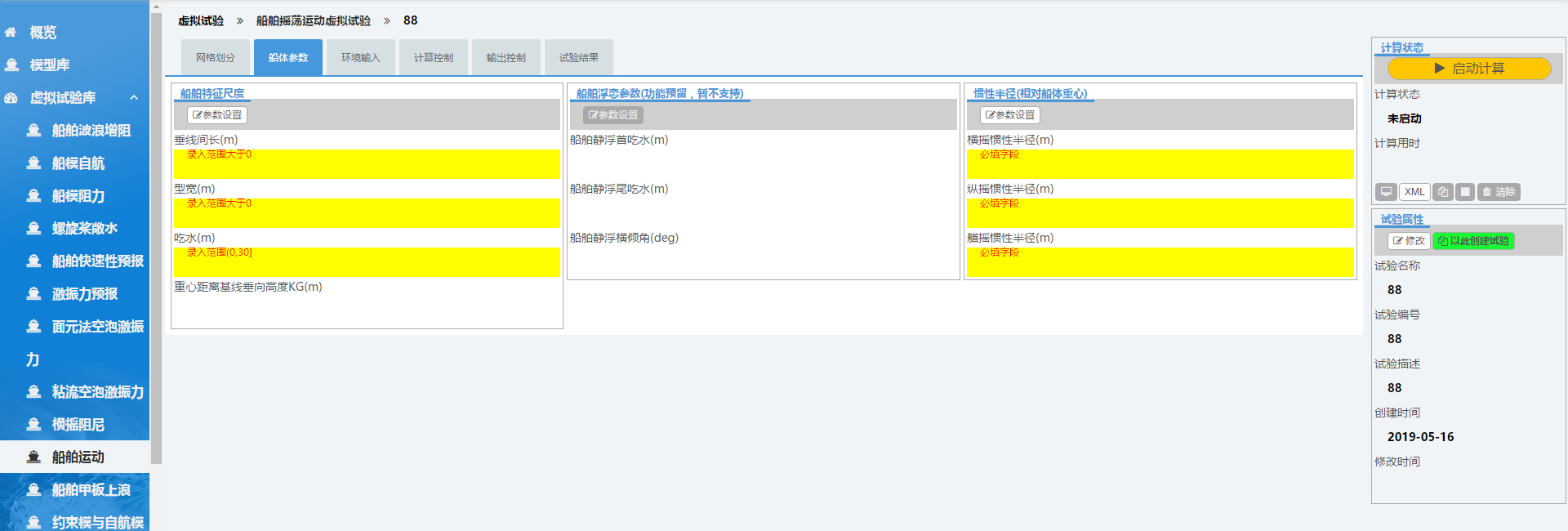
2.2 船体参数
在“船体参数”标签中,点击船舶特征尺度和惯性半径下的参数设置按钮,进行参数输入。这里请先填写船舶特征尺度(第一个填写垂线间长),再填写惯性半径。
2.3 环境输入
点击“环境输入”标签,可进入如下图所示页面。点击航速和波浪下的“参数设置”按钮。不同航速和波浪频率间用逗号隔开。

2.4 计算控制
点击“计算控制”标签,可进入如下图所示页面,通过点击“参数设置”按钮,填写相关参数。阻尼控制系数根据需要选择方法。
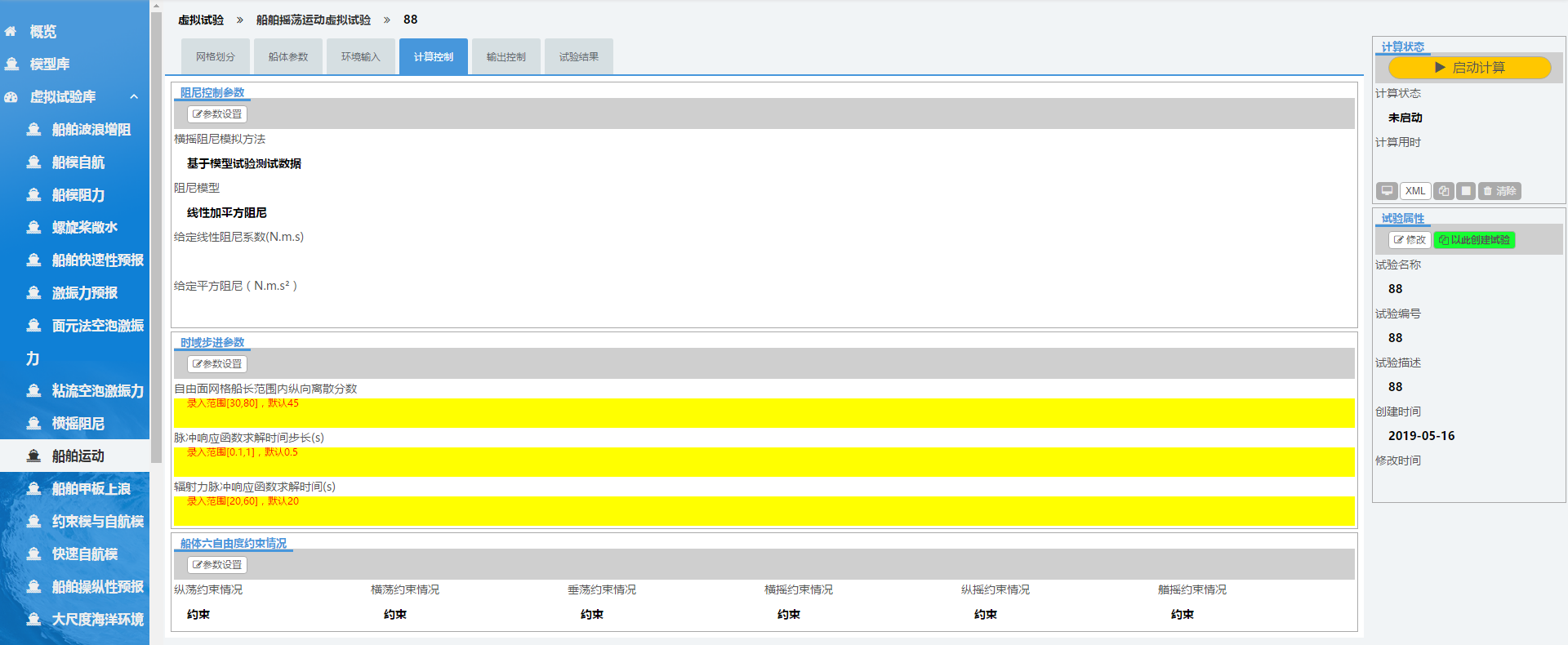
2.5 输出控制
点击“输出控制”标签,可进入如下图所示页面,可以对相关系数等参数进行设置。通过点击新建和删除来增加或减少参数。位移、速度、加速度点坐标可以不同,若要输入,三类点坐标都需要填写。
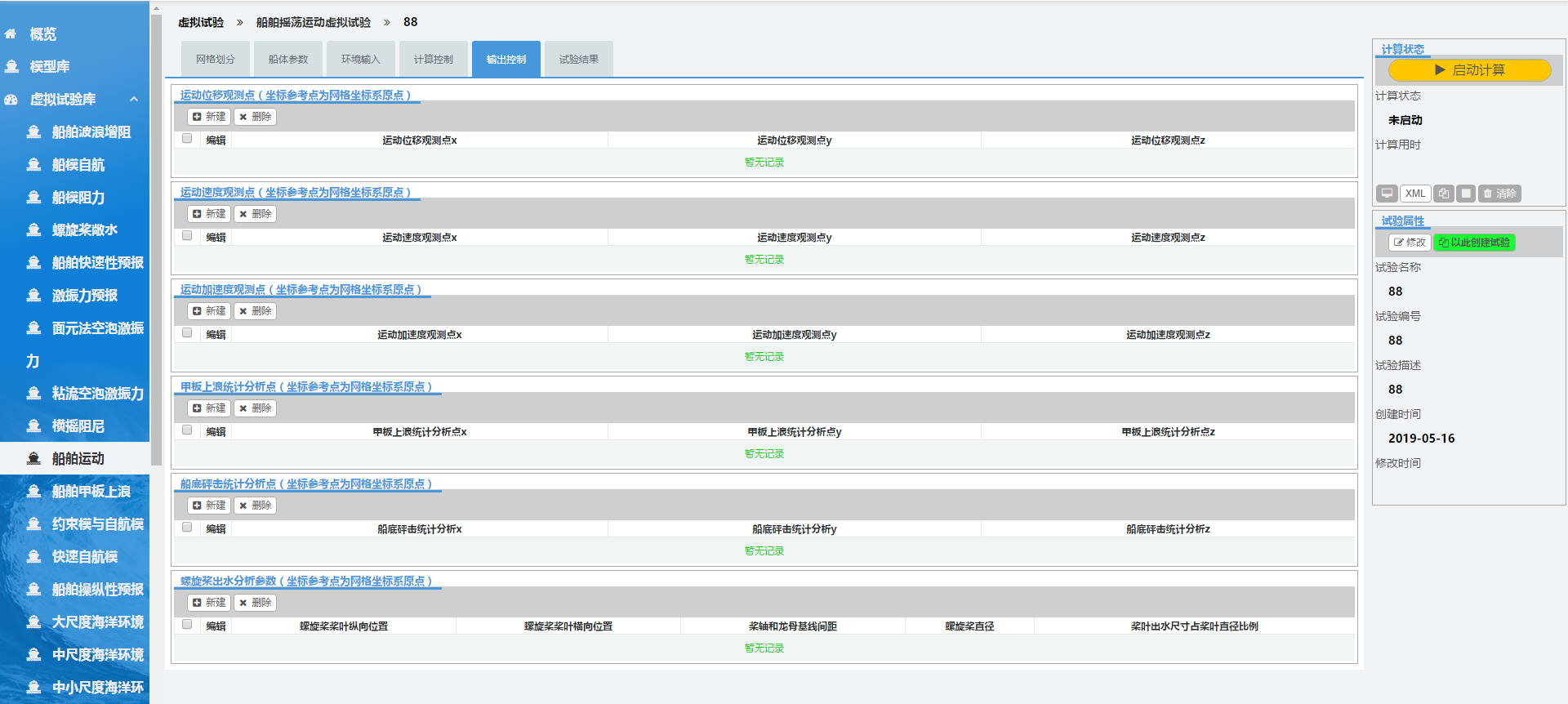
3. 计算求解
启动计算
点击“启动计算”按钮。
会弹出启动确认对话框,点击确定按钮即可启动计算。界面可看到求解时间。
4 结果展示
点击“试验结果”标签,可进入如下图所示页面。
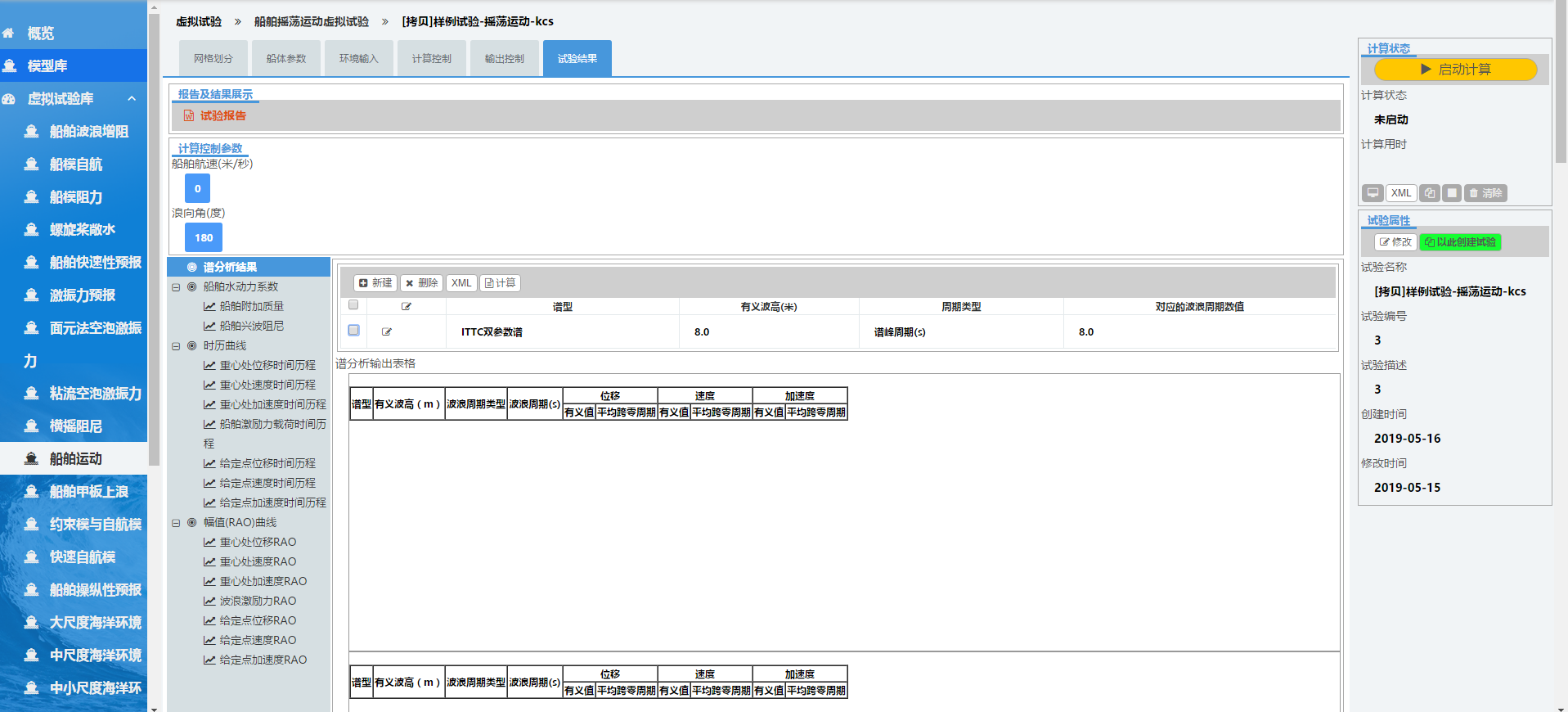
点击左侧曲线名称,可以得到结果曲线。可以在曲线上方的按钮进行切换。

进行谱分析时,点击左侧谱分析结果小标签,出现界面。
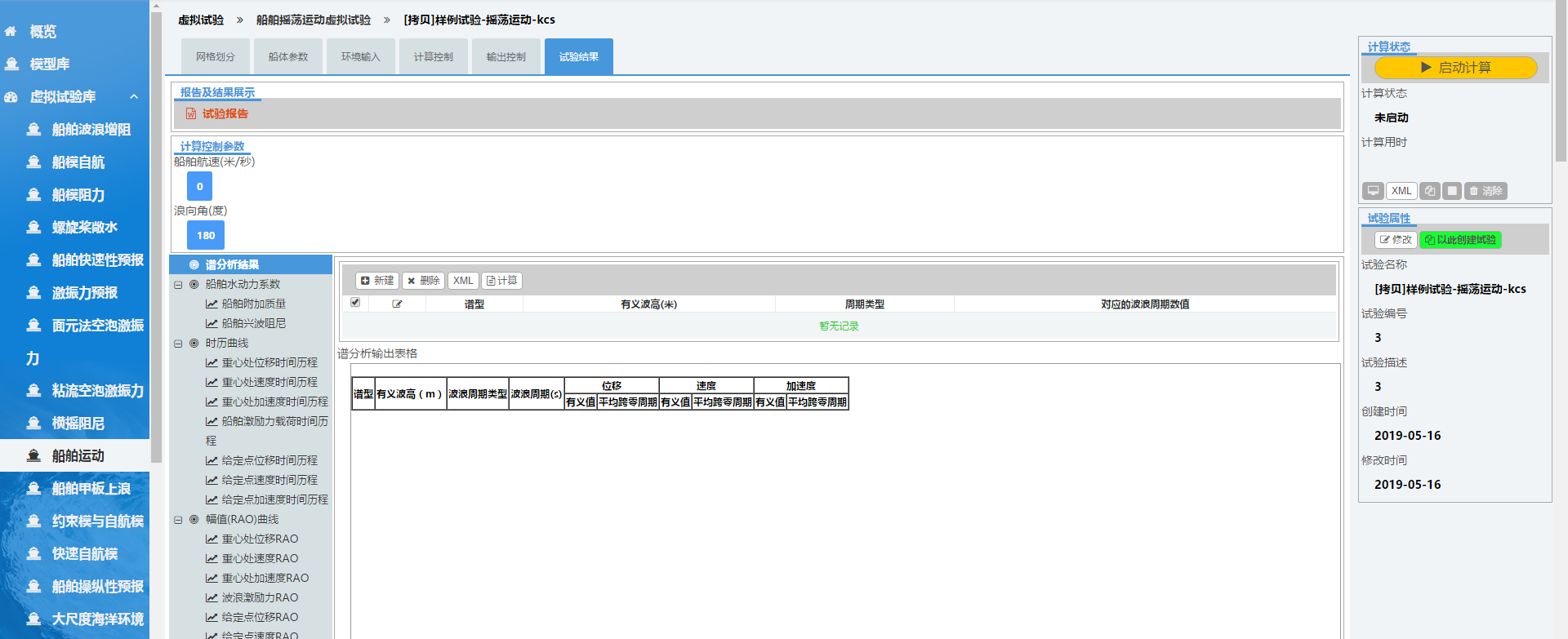
点击新建,选择谱类型等参数,创建不规则波,用删除按钮可以删除不规则波。完成后,点击计算,选择确定,进行谱分析。这里删除和新建后都要点击计算。进行谱分析前要完成规则波的计算。
点击试验报告,可以创建报告,点击确定,可以下载。

参考资料
开始试验1. 参考文献
[1]陈纪康,段文洋,朱鑫.三维泰勒展开边界元方法及其数值验证[J].水动力学研究与进展A辑,2013,28(04):482-485.
[2]段文洋,陈纪康,赵彬彬.基于泰勒展开边界元法的深水浮体二阶平均漂移力计算[J].哈尔滨工程大学学报,2015,36(03):302-306.
[3] 陈纪康. 基于泰勒展开边界元法的水波与浮体二阶水动力问题数值模拟[D].哈尔滨工程大学,2015.
[4]朱城锜. 基于泰勒展开边界元方法的肥大型船运动及波浪增阻时域计算敏感参数分析.第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集(下册)[C],2017:6.
[5]段文洋,王隶加,陈纪康,赵彬彬.基于泰勒展开边界元法的近水面潜艇垂向二阶波浪力(矩)计算[J].哈尔滨工程大学学报,2017,38(01):8-12.
[6] 郜振纲. 脉冲响应函数和泰勒展开边界元法相结合的船舶运动计算分析[A].第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集(下册)[C],2017:6.
[7] 陈纪康,王慧,马山,段文洋,王隶加.基于泰勒展开边界元方法的某半潜式平台水动力计算分析[J].哈尔滨工程大学学报,2018,39(09):1431-1437.
[8]汪小佳. 有航速浮体在波浪上运动的时域计算及统一表达的Kramers-Kronig关系的推导与验证[A].第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集(下册)[C],2017:10.
[9]周文俊. 基于三维时域格林函数高阶面元法的船体运动计算[A].纪念《船舶力学》创刊二十周年学术会议论文集[C].中国造船工程学会船舶力学学术委员会,2017:11.
[10]唐恺,朱仁传,缪国平,范菊.Domain Decomposition and Matching for Time-Domain Analysis of Motions of Ships Advancing in Head Sea[J].China Ocean Engineering,2014,28(04):433-444.
[11]方昭昭,赵丙乾,朱仁传.顶浪中船舶运动的数值模拟与波浪增阻计算[J].中国造船,2014,55(02):8-17.
[12]唐恺,朱仁传,缪国平,范菊.波浪中浮体运动的时域混合格林函数法[J].上海交通大学学报,2014,48(04):508-514.
[13]洪亮. 航行船舶频域运动计算比较与分析[A].第二十五届全国水动力学研讨会暨第十二届全国水动力学学术会议文集(下册)[C].2013:8.
[14]方昭昭,赵丙乾,金武雷,朱仁传.顶浪中船舶水动力计算与运动模拟研究[J].中国舰船研究,2013,8(05):33-40.
[15]唐恺. 基于混合格林函数法的波浪中船舶时域运动计算[A].2013年船舶水动力学学术会议论文集[C].2013:12.
[16]洪亮,朱仁传,缪国平,范菊.三维频域有航速格林函数的数值计算与分析[J].水动力学研究与进展A辑,2013,28(04):423-430.
[17]方昭昭,朱仁传,缪国平,杨雄辉.基于数值波浪水池的波浪中船舶水动力计算[J].水动力学研究与进展A辑,2012,27(05):515-524.
[18] Nakos D.E., Ship wave patterns and motions by a three dimensional Rankine panel method. PhD. Thesis, MIT, 1990.
[19] Kring D.C., Time domain ship motions by a three dimensional Rankine panel method, PhD. Thesis, MIT, 1994.
[20] Huang Y.F., Nonlinear ship motions by a Rankine panel method, PhD. Thesis, MIT, 1997.
[21] Zhang X., Beck R.F., Three-dimensional large amplitude body motions in waves. Journal of Offshore Mechanics and Arctic Engineering, 130(4), 2008.
[22] Song M.J., Kim K.H. and Kim Y.H., Numerical analysis and validation of weakly nonlinear ship motions and structural loads on a modern containership, Ocean Engineering, 38, 77-87, 2011.
[23] Iwashita, H., Bertram, V., Numerical study on the influence of the steady flow in seakeeping. 12th Int. Workshop on Water Waves and Floating Bodies, France, 1997.
[24] Iwashita, H., Ito, A., Seakeeping computations of a blunt ship capturing the influence of the steady flow. Ship Technol Res, 45, 4, 159-171, 1998.
[25] Chen X.B., Diebold L., Doutreleau Y., New green function method to predict waveinduced ship motions and loads, Proc. of 23rd Symposium on Naval Hydrodynamics, Val DE Reuil, France, 18-33, 2000.
[26] Duan, W.Y., Price, W.G., A numerical method to solve the mj-terms of a submerged body with forward speed. Int J Numer Methods Eng, 40, 655-667, 2002.
[27] Teng, B., Bai, W., Dong, G., Simulation of second-order radiation of 3D bodies in time domain by a B-spline method. Proc Int Offshore Polar Eng Conf, 12, 487-493, 2002.
[28] Engsig-Karup, A. P., Bingham, H. B., Boundary-fitted solutions for 3D nonlinear water wave-structure interaction, 24th Int. Workshop on Water Waves and Floating Bodies, Russia, 2009.
[29]He G.H., Kashiwagi M., Time Domain Simulation of Steady Ship Wave Problem by a Higher-Order Boundary Element Method. Proceedings of 22th International Offshore and Polar Engineering Conference. Greese, 2012.
[30] He G.H., Kashiwagi M., A time-domain higher-order boundary element method for 3D forward speed radiation and diffraction problems. Journal of marine science and technology, 19, 228-244, 2014.
[31]Duan W.Y., Dai Y.S.,Time-domain calculation of hydrodynamic forces on ships with large flare, International Shipbuilding Progress, 46(446), 223-232, 1999.
2. 研究团队
哈尔滨工程大学 段文洋等
上海交通大学 朱仁传等
韩国国立首尔大学 Yonghwan Kim等
日本大坂大学 柏木正等
美国密歇根大学 Beck R.F.等
法国BV船级社 陈晓波等
3. 研究进展
在船舶耐波性分析领域,势流边界元方法由于计算稳定、精度可靠,计算效率高等优点得到了广泛的应用。
当前三维势流有航速边界元法是船舶势流边界元方法应用的难点和热点,而三维时域势流边界元方法是其中的主流方法。
应用三维时域势流边界元方法求解船舶等海洋浮体辐射和绕射的水动力边值问题当前采用如下的三种方法。第一种方法是基于解析的三维时域瞬态自由面格林函数方法。第二种方法是基于简单格林函数的Rankine源方法。第三种方法是将三维瞬态自由面格林函数与简单格林函数Rankine源法结合的内外流域匹配边界元方法。
三维瞬态自由面格林函数法可自动满足线性自由面边界条件,仅需在船体表面建立流场势满足的边界积分方程,因此时域格林函数方法在国内外被不少学者用于船舶水动力计算研究。如Liapis and Beck(1985)对有航速辐射问题进行了研究。把速度势分解成瞬时效应和记忆效应两部分,应用时域格林函数建立了速度势满足的边界积分方程。国内的张亮、戴遗山,段文洋,王大云,朱海荣等应用时域格林函数法对船舶与海洋浮体的水动力进行了深入研究。目前采用三维时域自由面格林函数应用于船舶有航速水动力分析对非直壁船存在边界积分方程求解振荡发散的问题,阻碍了该种方法在大外飘船水动力分析中的工程应用。
Rankine源方法是在物面和自由面上都分布奇点的一种计算方法。与自由面格林函数方法相比,该方法在建立流场速度势边界积分方程时需在自由液面布置源汇及偶极,以满足自由面条件;在远场也需设置合适的辐射条件,以使流场数值解符合物理实际。但正因为在自由面布置奇点,使得将该方法拓展至非线性边值问题变得容易。Rankine源方法首先是由Gadd(1976)和Dawson(1977)在研究Kelvin波和兴波阻力时提出的,Chapman(1981)将其应用于时域有航速计算上。Kring等对时域Rankine面源法进行了全面研究,分析了船舶水动力数值计算中时间和空间离散的稳定性。采用Rankine源方法进行船舶有航速水动力分析方法已取得很大进展,发展了船舶耐波性和波浪载荷分析的工程预报软件,如WASIM,SWAN和WISH等。经过多年发展,Rankine源方法已经从全线性向瞬时物面及自由面的边值问题发展。
为了将时域自由面格林函数和Rankine源方法结合,学者们提出了内外流域匹配边界元方法。该方法通过引入一个虚拟控制面将船舶周围计算域分为内域和外域两个部分。在船舶周围的内域采用Rankine源方法建立边界积分方程,在外域采用三维时域格林函数方法建立边界积分方程,通过内外域流场在控制面的速度势和法向速度匹配条件将内外域边界积分方程联立求解。该方法将时域自由面格林函数和Rankine源方法的各自优势相结合,可自动满足外部流域的船舶辐射波外传条件,同时解决了大外飘船自由面格林函数法求解带来的流场求解发散问题。段文洋、陈纪康(2017)采用三维时域势流边界元方法用于船舶有航速水动力分析,为了解决斜壁船水动力求解发散问题,建立了内外流域匹配边界元方法。在船体附近内部流域,发展了三维泰勒展开边界元方法用于离散船体和自由液面的边界积分方程,实现了船体扰动流场速度和速度势高阶导数的准确数值求解,从而发展了船舶三维时域泰勒展开边界元求解数值算法,在集装箱船、散货船、油船等三大主力船型船舶波浪增阻和耐波性运动分析中获得应用。
4. 实用工具
WASIM,WISH,SWAN,LAMP等
咨询电话:0451-82569306
版权所有:数值水池 信息维护:数值水池创新团队 地址:哈尔滨市南岗区南通大街145号 邮编:150001
联系我们:nwt@hrbeu.edu.cn;zhaobin2_1984@163.com 黑ICP备17002841号-10 公安备案号:23010302000541










